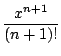 =
= 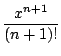 =
=
Comment en déduire une valeur approchée de ex? Il suffira d'arrêter
la sommation lorsque
R : = xn+1/(n + 1)! si x < 0 ou lorsque
R : = exxn+1/(n + 1)! si x > 0 est inférieur à
l'erreur absolue souhaitée, le plus tôt étant le mieux pour des
raisons d'efficacité et pour éviter l'accumulation d'erreurs
d'arrondi.
Si on veut connaitre ex à une erreur relative
![]() donnée
(par exemple
donnée
(par exemple
![]() = 2-53 pour stocker le résultat dans un double)
il suffit que
R/ex <
= 2-53 pour stocker le résultat dans un double)
il suffit que
R/ex < ![]() , donc si x est positif, il suffit
que
xn+1/(n + 1)! <
, donc si x est positif, il suffit
que
xn+1/(n + 1)! < ![]() , on peut donc arrêter la sommation
lorsque le terme suivant est plus petit que
, on peut donc arrêter la sommation
lorsque le terme suivant est plus petit que
![]() .
On observe que plus x est grand, plus n devra
être grand pour réaliser le test d'arrêt, ce qui est facheux.
On peut utiliser les propriétés de la fonction exponentielle
pour éviter ce problème, si on connait une valeur approchée
de ln(2) on effectue la division euclidienne de x par ln(2)
avec reste symétrique :
.
On observe que plus x est grand, plus n devra
être grand pour réaliser le test d'arrêt, ce qui est facheux.
On peut utiliser les propriétés de la fonction exponentielle
pour éviter ce problème, si on connait une valeur approchée
de ln(2) on effectue la division euclidienne de x par ln(2)
avec reste symétrique :
Il faut toutefois noter que ln(2) n'étant pas connu exactement,
on commet une erreur d'arrondi absolu sur r d'ordre a![]() ,
où
,
où ![]() est l'erreur relative sur ln(2),
il faut donc ajouter une erreur d'arrondi relative de
x/ln(2)
est l'erreur relative sur ln(2),
il faut donc ajouter une erreur d'arrondi relative de
x/ln(2)![]() qui peut devenir grande si x est grand. Puis il faut ajouter
la somme des erreurs d'arrondi due au calcul de er, que l'on
peut minimiser en utilisant la méthode de Horner pour évaluer
Tn(f )(r) (car elle commence par sommer les termes de plus haut degré
qui sont justement les plus petits termes de la somme).
Les coprocesseurs arithmétiques qui implémentent la fonction exponentielle
ont un format de représentation interne des double avec une mantisse
plus grande que celle des double (par exemple 80 bits au lieu de 52),
et une table contenant des constantes dont ln(2) avec cette précision,
le calcul de ex par cette méthode entraine donc seulement une erreur
relative d'arrondi au plus proche sur le résultat converti en double
(donc de 2-53).
qui peut devenir grande si x est grand. Puis il faut ajouter
la somme des erreurs d'arrondi due au calcul de er, que l'on
peut minimiser en utilisant la méthode de Horner pour évaluer
Tn(f )(r) (car elle commence par sommer les termes de plus haut degré
qui sont justement les plus petits termes de la somme).
Les coprocesseurs arithmétiques qui implémentent la fonction exponentielle
ont un format de représentation interne des double avec une mantisse
plus grande que celle des double (par exemple 80 bits au lieu de 52),
et une table contenant des constantes dont ln(2) avec cette précision,
le calcul de ex par cette méthode entraine donc seulement une erreur
relative d'arrondi au plus proche sur le résultat converti en double
(donc de 2-53).
Notons que en général x lui-même
a déjà été arrondi ou n'est connu qu'avec une précision relative.
Or si x > 0 est connu avec une erreur relative de
![]() (donc une erreur absolue de
(donc une erreur absolue de
![]() | x|, alors
| x|, alors
Exercice : refaire les mêmes calculs pour les fonction sinus ou cosinus.
On utilise par exemple
sin(x + ![]() ) = - sin(x),
sin(- x) = - sin(x),
sin(x) = cos(
) = - sin(x),
sin(- x) = - sin(x),
sin(x) = cos(![]() /2 - x) pour se ramener au calcul de sin(x)
ou de cos(x) sur [0,
/2 - x) pour se ramener au calcul de sin(x)
ou de cos(x) sur [0,![]() /4].
/4].
 , cos(x) =
, cos(x) = Cette méthode a toutefois ces limites, car il peut devenir impraticable de calculer la dérivée n-ième d'une fonction (par exemple avec tan(x)), et encore plus de la majorer. D'où l'intérêt de développer une théorie des fonctions qui sont égales à leur développement de Taylor à l'infini d'une part, et d'avoir d'autres méthodes pour majorer le reste, nous présentons ici le cas des séries alternées.