


suivant: Développement de Taylor, séries
monter: Suites itératives et applications
précédent: Le point fixe
Index
La méthode de Newton est une méthode de résolution de l'équation
f (x) = 0, attention à la différence avec le théorème du point fixe
qui permet de résoudre numériquement f (x) = x.
Si x0 est proche de la racine r
on peut faire un développement de Taylor à l'ordre 1 de la
fonction f en x0 :
f (x) = f (x0) + (x - x0)f'(x0) + O((x - x0)2)
Pour trouver une valeur approchée de r, on ne garde que la partie
linéaire du développement, on résout :
f (
r) = 0
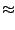 f
f (
x0) + (
r -
x0)
f'(
x0)
donc (si
f'(x0) 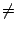 0) :
0) :
r 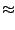 x0
x0 -
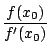
Graphiquement, cela revient à tracer la tangente à la courbe représentative
de f et à chercher où elle coupe l'axe des x.
On considère donc la suite récurrente définie par une valeur u0
proche de la racine et par la relation :
un+1 =
un -
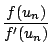
Il y a deux théorèmes importants, l'un d'eux prouve que
si u0 est ``assez proche'' de r alors la suite un converge vers r,
malheureusement il est difficile de savoir en pratique si on est
``assez proche'' de u0 pour que ce théorème s'applique. Le second
théorème donne un critère pratique facile à vérifier qui assure
la convergence, il utilise les propriétés de convexité de la fonction.
Démonstration : on a
un+1 -
r =
un -
r -
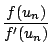
=
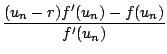
En appliquant un développement de Taylor de f en un à l'ordre 2,
on obtient pour un réel 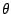 situé entre r et un :
situé entre r et un :
0 =
f (
r) =
f (
un) + (
r -
un)
f'(
un) + (
r -
un)
2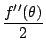
(
un -
r)
f'(
un) -
f (
un) = (
un -
r)
2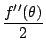
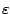 , r +
, r + 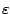 ]
contenant strictement r et tel que | f''| < M et | 1/f'| < m
sur
[r -
]
contenant strictement r et tel que | f''| < M et | 1/f'| < m
sur
[r - 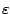 , r +
, r + 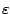 ] (c'est toujours possible car
f'' et 1/f' sont continues au voisinage de r puisque
f'(r)
] (c'est toujours possible car
f'' et 1/f' sont continues au voisinage de r puisque
f'(r) 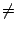 0).
Si un est dans cet intervalle, alors
0).
Si un est dans cet intervalle, alors 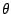 aussi donc
aussi donc
|
un+1 -
r|
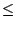
|
un -
r|
2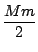
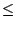
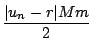
|
un -
r|,
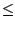
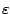 , on diminue si nécessaire
, on diminue si nécessaire
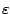 pour avoir
pour avoir
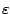 < 2/(Mm), on a alors :
< 2/(Mm), on a alors :
|
un+1 -
r|
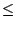 k
k|
un -
r|,
k =
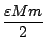
< 1
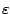 , r +
, r + 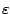 ]
ce qui permettra de refaire le même raisonnement au rang
suivant, et d'autre part
on a une convergence au moins géométrique vers r (en fait bien meilleure
lorsqu'on est proche de r grace au carré dans | un - r|2).
]
ce qui permettra de refaire le même raisonnement au rang
suivant, et d'autre part
on a une convergence au moins géométrique vers r (en fait bien meilleure
lorsqu'on est proche de r grace au carré dans | un - r|2).
Remarque : ce théorème se généralise sur
 et même sur
et même sur
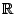 n.
n.
Exemple : pour calculer 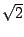 , on écrit l'équation x2 - 2 = 0
qui a
, on écrit l'équation x2 - 2 = 0
qui a 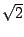 comme racine simple sur I = [1/2, 2],
on obtient la suite récurrente
comme racine simple sur I = [1/2, 2],
on obtient la suite récurrente
un+1 =
un -
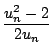
Si on prend 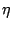 = 1/2, on a f' = 2x et f'' = 2
donc on peut prendre M = 2 et m = 1 car
| 1/f'|
= 1/2, on a f' = 2x et f'' = 2
donc on peut prendre M = 2 et m = 1 car
| 1/f'| 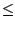 1 sur
[
1 sur
[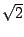 -1/2,
-1/2,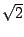 + 1/2]. On a 2/(mM) = 1, on peut donc
prendre
+ 1/2]. On a 2/(mM) = 1, on peut donc
prendre
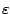 = 1/2, la suite convergera pour tout
u0
= 1/2, la suite convergera pour tout
u0 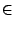 [
[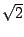 -1/2,
-1/2,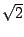 + 1/2].
+ 1/2].
Plus générallement, on peut calculer une racine k-ième d'un réel a
en résolvant
f (x) = xk - a par la méthode de Newton.
L'inconvénient de ce théorème
est qu'il est difficile de savoir si la valeur de départ qu'on
a choisie se trouve suffisamment près d'une racine pour que
la suite converge. Pour illustrer le phénomène,
on peut par exemple colorer les points du plan
complexe en n + 1 couleurs selon que la suite définie par la méthode
de Newton converge vers l'une des n racines d'un polynôme de degré
n fixé au bout de par exemple 50 itérations (la n + 1-ième couleur
servant aux origines de suite qui ne semblent pas converger).
Passons maintenant à un critère très utile en pratique :
Définition 4 (convexité)
Une fonction f continument dérivable sur un intervalle I de
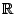 est dite convexe si son graphe est au-dessus de la tangente en tout point
de I.
est dite convexe si son graphe est au-dessus de la tangente en tout point
de I.
Il existe un critère simple permettant de savoir si
une fonction de classe C2 est convexe :
Théorème 3
Si f est C2 et
f'' 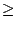 0 sur I alors f est convexe.
0 sur I alors f est convexe.
Démonstration :
L'équation de la tangente au graphe en x0 est
y = f (x0) + f'(x0)(x - x0)
Soit
g(x) = f (x) - (f (x0) + f'(x0)(x - x0))
on a :
g(
x0) = 0,
g'(
x) =
f'(
x) -
f'(
x0),
g'(
x0) = 0,
g'' =
f''
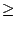
0
donc g' est croissante, comme g'(x0) = 0, g' est négative
pour x < x0 et positive pour x > x0, donc g est décroissante
pour x < x0 et croissante pour x > x0. On conclut alors que
g 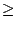 0 puisque g(x0) = 0. Donc f est bien au-dessus
de sa tangente.
0 puisque g(x0) = 0. Donc f est bien au-dessus
de sa tangente.
On arrive au deuxième théorème sur la méthode de Newton
Théorème 4
Si
f (r) = 0, f'(r) > 0 et si
f'' 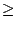 0 sur [r, b] alors
pour tout
u0
0 sur [r, b] alors
pour tout
u0 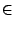 [r, b] la suite de la méthode de Newton
[r, b] la suite de la méthode de Newton
un+1 =
un -
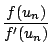
,
est définie, décroissante, minorée par r et converge vers
r. De plus
Démonstration :
On a
f'' 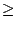 0 donc si f'(r) > 0 alors f' > 0
sur [r, b], f est donc strictement croissante sur [r, b]
on en déduit que f > 0 sur ]r, b] donc
un+1
0 donc si f'(r) > 0 alors f' > 0
sur [r, b], f est donc strictement croissante sur [r, b]
on en déduit que f > 0 sur ]r, b] donc
un+1 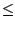 un.
Comme la courbe représentative de f est au-dessus de la tangente,
on a
un+1
un.
Comme la courbe représentative de f est au-dessus de la tangente,
on a
un+1 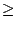 r (car un+1 est l'abscisse du point
d'intersection de la tangente avec l'axe des x).
La suite un est donc décroissante minorée par r, donc convergente
vers une limite l
r (car un+1 est l'abscisse du point
d'intersection de la tangente avec l'axe des x).
La suite un est donc décroissante minorée par r, donc convergente
vers une limite l 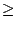 r. À la limite, on a
r. À la limite, on a
l =
l -

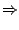 f
f (
l )= 0
donc l = r car f > 0 sur ]r, b].
Comme (un) est décroissante, on a bien
0 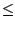 un - r,
pour montrer l'autre inégalité, on applique le théorème
des accroissements finis, il existe
un - r,
pour montrer l'autre inégalité, on applique le théorème
des accroissements finis, il existe
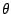
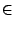 [r, un] tel que
[r, un] tel que
f (
un) -
f (
r) = (
un -
r)
f'(
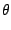
)
comme f (r) = 0, on a
un -
r =
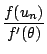
et la deuxième inégalité du théorème
en découle parce que f' est croissante.
Variantes :
Il existe des variantes, par exemple si f'(r) < 0 et
f'' 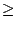 0
sur [a, r]. Si
f''
0
sur [a, r]. Si
f'' 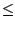 0, on considère g = - f.
0, on considère g = - f.
Application :
On peut calculer la valeur approchée de la
racine k-ième d'un réel a > 0 en appliquant ce deuxième
théorème. En effet si
a > 0, alors xk - a est 2 fois continument dérivable et
de dérivée première kxk-1 et
seconde
k(k - 1)xk-2 strictement positives sur
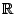 + * (car k
+ * (car k 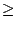 2).
Il suffit donc de prendre une valeur de départ u0 plus grande que
la racine k-ième, par exemple 1 + a/k (en effet
(1 + a/k)k
2).
Il suffit donc de prendre une valeur de départ u0 plus grande que
la racine k-ième, par exemple 1 + a/k (en effet
(1 + a/k)k 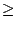 1 + ka/k = 1 + a).
En appliquant l'inégalité du théorème, on a :
1 + ka/k = 1 + a).
En appliquant l'inégalité du théorème, on a :
Pour avoir une valeur approchée de
![$ \sqrt[k]{{a}}$](img63.png) à
à
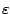 près,
on peut donc choisir comme test d'arrêt
Par exemple pour
près,
on peut donc choisir comme test d'arrêt
Par exemple pour 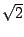 , le test d'arrêt serait
un2 -2
, le test d'arrêt serait
un2 -2 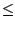 2
2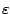 .
.



suivant: Développement de Taylor, séries
monter: Suites itératives et applications
précédent: Le point fixe
Index
Retour à la page principale de mat249
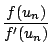
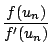 , | u0 - r|
, | u0 - r| ![]() M et
| 1/f'|
M et
| 1/f'| ![]() m sur un intervalle
[r -
m sur un intervalle
[r - ![]() , r +
, r + ![]() ] contenu dans I, alors on peut prendre tout réel
] contenu dans I, alors on peut prendre tout réel
![]() > 0 tel que
> 0 tel que
![]() < 2/(mM) et
< 2/(mM) et
![]()
![]()
![]() .
.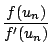 =
= 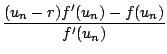
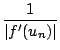
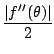
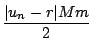 | un - r|,
| un - r|,
![]() et même sur
et même sur
![]() n.
n.
![]() , on écrit l'équation x2 - 2 = 0
qui a
, on écrit l'équation x2 - 2 = 0
qui a ![]() comme racine simple sur I = [1/2, 2],
on obtient la suite récurrente
comme racine simple sur I = [1/2, 2],
on obtient la suite récurrente
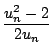
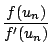 ,
,
![]() 0 donc si f'(r) > 0 alors f' > 0
sur [r, b], f est donc strictement croissante sur [r, b]
on en déduit que f > 0 sur ]r, b] donc
un+1
0 donc si f'(r) > 0 alors f' > 0
sur [r, b], f est donc strictement croissante sur [r, b]
on en déduit que f > 0 sur ]r, b] donc
un+1 ![]() un.
Comme la courbe représentative de f est au-dessus de la tangente,
on a
un+1
un.
Comme la courbe représentative de f est au-dessus de la tangente,
on a
un+1 ![]() r (car un+1 est l'abscisse du point
d'intersection de la tangente avec l'axe des x).
La suite un est donc décroissante minorée par r, donc convergente
vers une limite l
r (car un+1 est l'abscisse du point
d'intersection de la tangente avec l'axe des x).
La suite un est donc décroissante minorée par r, donc convergente
vers une limite l ![]() r. À la limite, on a
r. À la limite, on a
![]() un - r,
pour montrer l'autre inégalité, on applique le théorème
des accroissements finis, il existe
un - r,
pour montrer l'autre inégalité, on applique le théorème
des accroissements finis, il existe
![]()
![]() [r, un] tel que
[r, un] tel que
![]() 0
sur [a, r]. Si
f''
0
sur [a, r]. Si
f'' ![]() 0, on considère g = - f.
0, on considère g = - f.
![]() + * (car k
+ * (car k ![]() 2).
Il suffit donc de prendre une valeur de départ u0 plus grande que
la racine k-ième, par exemple 1 + a/k (en effet
(1 + a/k)k
2).
Il suffit donc de prendre une valeur de départ u0 plus grande que
la racine k-ième, par exemple 1 + a/k (en effet
(1 + a/k)k ![]() 1 + ka/k = 1 + a).
En appliquant l'inégalité du théorème, on a :
1 + ka/k = 1 + a).
En appliquant l'inégalité du théorème, on a :
![$\displaystyle {\frac{{u_n^k - a}}{{k\sqrt[k]{a}^{k-1} }}}$](img60.png)
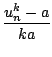
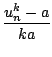 (1 +
(1 +