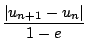


suivant: La méthode de Newton.
monter: Suites itératives et applications
précédent: Suites itératives et applications
Index
Soit f une fonction continue sur un intervalle I = [a, b] de
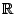 , et
à valeurs dans I (attention à bien choisir I pour que l'image
de I par f reste dans I).
On s'intéresse à la suite
, et
à valeurs dans I (attention à bien choisir I pour que l'image
de I par f reste dans I).
On s'intéresse à la suite
un+1 = f (un), u0 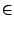 I I |
(1) |
Supposons que un converge vers une limite l 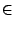 I lorsque
n
I lorsque
n  +
+ 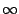 , alors la limite doit vérifier
, alors la limite doit vérifier
f (l )= l
puisque f est continue. On dit que l est un point fixe de f.
Ceci amène à l'idée d'utiliser ces suites pour résoudre numériquement
l'équation f (x) = x. Nous allons donner un théorème permettant
d'assurer que la suite (1) converge, et que la limite
est l'unique solution de f (l )= l sur I.
Définition 3
On dit que f est contractante de rapport k < 1 sur I si
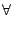 x
x,
y 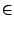 I
I, |
f (
y) -
f (
x)|
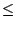 k
k|
y -
x|
En pratique, les fonctions f que l'on considèrera seront continument
dérivables, donc d'après le théorème des accroissements finis
f (
y) -
f (
x) =
f'(
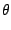
)(
y -
x),
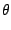
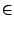
[
x,
y]
ainsi pour vérifier que f est contractante, on étudie la valeur absolue
de f' sur I, il suffit de montrer que cette valeur absolue
est strictement inférieure à un réel k < 1 pour conclure (il faut
donc chercher le maximum de | f'| sur I. Attention, il s'agit du
maximum de | f'| et pas du maximum de f', ce qui revient à chercher
le maximum de f' et de - f').
On a alors le
Théorème 1 (du point fixe)
si f est contractante de I = [a, b]
dans I de rapport k
alors la suite (1) converge vers l'unique
solution de f (l )= l dans I. On a de plus les encadrements :
| un - l| 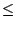 kn| b - a|, | un - l| kn| b - a|, | un - l| 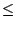 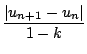 |
(2) |
Démonstration : Tout d'abord si f est contractante, on montre à partir
de la définition de la continuité que f est continue.
Soit
g(x) = f (x) - x, alors g est continue, positive en a et négative
en b, il existe donc l 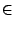 [a, b] tel que g(l )= 0 (théorème des
valeurs intermédiaires). Soit un une suite définie par
(1). On a alors pour tout n
[a, b] tel que g(l )= 0 (théorème des
valeurs intermédiaires). Soit un une suite définie par
(1). On a alors pour tout n
|
un+1 -
l| = |
f (
un) -
f (
l )|
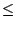 k
k|
un -
l|
|
un -
l|
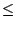 kn
kn|
u0 -
l|
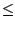 kn| a - b|.
Comme
k
kn| a - b|.
Comme
k 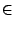 [0, 1[, la suite géométrique kn converge vers 0
lorsque n tend vers l'infini, donc un tend vers l.
Notons que l est unique car si l' est une autre solution
alors
| l - l'| = | f (l )- f (l')|
[0, 1[, la suite géométrique kn converge vers 0
lorsque n tend vers l'infini, donc un tend vers l.
Notons que l est unique car si l' est une autre solution
alors
| l - l'| = | f (l )- f (l')| 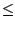 k| l - l'| donc
(1 - k)| l - l'|
k| l - l'| donc
(1 - k)| l - l'| 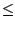 0,
or 1 - k > 0 et
| l - l'|
0,
or 1 - k > 0 et
| l - l'| 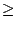 0 donc | l - l'| doit être nul.
Passons à la preuve de la majoration (2) qui est importante
en pratique car elle donne un test d'arrêt de calcul des
termes de la suite récurrente, on écrit pour m > 0 :
0 donc | l - l'| doit être nul.
Passons à la preuve de la majoration (2) qui est importante
en pratique car elle donne un test d'arrêt de calcul des
termes de la suite récurrente, on écrit pour m > 0 :
un - l = un - un+1 + un+1 - un+2 + ... + un+m-1 - un+m + um - l
puis on majore avec l'inégalité triangulaire
|
un -
l|
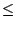
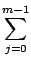
|
un+j -
un+j+1| + |
um -
l|
|
un -
l|
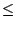
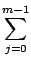 kj
kj|
un -
un+1| + |
um -
l|
|
un -
l|
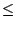
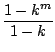
|
un -
un+1| + |
um -
l|
Exemples :
Cherchons une valeur approchée de 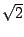 par cette méthode.
Il faut d'abord trouver une fonction f dont
par cette méthode.
Il faut d'abord trouver une fonction f dont 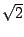 est un point
fixe, par exemple
est un point
fixe, par exemple
f (
x) =
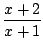
On vérifie que
f (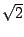 ) =
) = 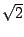 ), puis que
f' = - 1/(x + 2)2
donc f décroit. On va voir si les hypothèses du théorème du point
fixe s'appliquent sur par exemple [1, 2]. Comme f est décroissante
f ([1, 2]) = [f (2), f (1)] = [4/3, 3/2] qui est bien inclus dans [1, 2].
De plus f' est comprise entre
-1/(1 + 1)2 = - 1/4 et
-1/(2 + 1)2 = - 1/9 donc
| f'| < 1/4, f est contractante de rapport 1/4. On peut donc
itérer la suite à partir par exemple de u0 = 1 et on va converger
vers
), puis que
f' = - 1/(x + 2)2
donc f décroit. On va voir si les hypothèses du théorème du point
fixe s'appliquent sur par exemple [1, 2]. Comme f est décroissante
f ([1, 2]) = [f (2), f (1)] = [4/3, 3/2] qui est bien inclus dans [1, 2].
De plus f' est comprise entre
-1/(1 + 1)2 = - 1/4 et
-1/(2 + 1)2 = - 1/9 donc
| f'| < 1/4, f est contractante de rapport 1/4. On peut donc
itérer la suite à partir par exemple de u0 = 1 et on va converger
vers 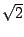 (en s'en rapprochant à chaque cran d'un rapport
inférieur à 1/4).
(en s'en rapprochant à chaque cran d'un rapport
inférieur à 1/4).
Considérons l'équation en x
x -
e sin(
x) =
t,
e 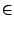
[0, 1[
c'est l'équation du temps utilisée en astronomie pour trouver la
position d'une planète sur son orbite elliptique (e étant l'excentricité
de l'ellipse).
Il n'y a pas de formule exacte permettant de calculer x en fonction de t.
Si on a une valeur numérique pour t, on peut trouver une valeur
numérique approchée de x par la méthode du point fixe, en réécrivant
l'équation sous la forme
f (x) = t + e sin(x) = x
On observe que f envoie
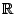 dans [t - e, t + e] donc on peut prendre
I = [t - e, t + e], de plus
| f'|
dans [t - e, t + e] donc on peut prendre
I = [t - e, t + e], de plus
| f'| 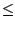 e < 1, f est contractante
de rapport
e
e < 1, f est contractante
de rapport
e 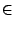 [0, 1[, le théorème s'applique, il suffit de
prendre une valeur initiale dans [t - e, t + e] et d'itérer la suite
jusqu'à obtenir la précision désirée. Par exemple si on veut une
valeur approchée de x à 10-6 près, il suffira que la différence
entre deux termes successifs de la suite un vérifie
[0, 1[, le théorème s'applique, il suffit de
prendre une valeur initiale dans [t - e, t + e] et d'itérer la suite
jusqu'à obtenir la précision désirée. Par exemple si on veut une
valeur approchée de x à 10-6 près, il suffira que la différence
entre deux termes successifs de la suite un vérifie
|
un+1 -
un|
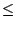
10
-6(1 -
e)
Cette méthode n'est pas toujours optimale, car la vitesse de convergence
vers la limite l est dite ``linéaire'' (le temps de calcul pour
avoir n décimales est proportionnel à n car il faut effectuer
un nombre proportionnel à n itérations, chaque itération faisant
gagner en précision de l'ordre du rapport k de contractance). Il existe
une méthode plus rapide lorsqu'on est proche de la racine ou lorsque
la fonction a des propriétés de convexité, c'est la méthode de Newton.



suivant: La méthode de Newton.
monter: Suites itératives et applications
précédent: Suites itératives et applications
Index
Retour à la page principale de mat249
![]() [a, b] tel que g(l )= 0 (théorème des
valeurs intermédiaires). Soit un une suite définie par
(1). On a alors pour tout n
[a, b] tel que g(l )= 0 (théorème des
valeurs intermédiaires). Soit un une suite définie par
(1). On a alors pour tout n
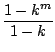 | un - un+1| + | um - l|
| un - un+1| + | um - l|
![]() par cette méthode.
Il faut d'abord trouver une fonction f dont
par cette méthode.
Il faut d'abord trouver une fonction f dont ![]() est un point
fixe, par exemple
est un point
fixe, par exemple