-1 cm 23cm @percent16.5cm 10pt 0pt
TP de mathématiques.Licence 2-Mat 2492012/13 |
Un logiciel de calcul formel permet de faire des manipulations algébriques sans avoir à effectuer d’approximation numérique, par exemple calculer la dérivée ou la primitive d’une fonction, résoudre certaines équations différentielles, etc. Il permet également de faire des calculs numériques, ainsi que des représentations graphiques, ... On en trouve :
Nous utiliserons Xcas qui est libre (donc gratuit) et de plus compatible avec Maple (pour ceux ayant déjà utilisé Maple, vous pourrez la plupart du temps utiliser les mêmes instructions et le même langage de programmation). Vous pouvez le télécharger à l’URL
www-fourier.ujf-grenoble.fr/~parisse/giac_fr.html
xcasfr du bureau.
xcas &.
xcas &
Lors de la première utilisation, choisissez Xcas lorsqu’on vous demande de choisir une syntaxe (sauf si vous connaissez le langage Maple). Nous donnons ici seulement le minimum de l’interface à connaitre pour commencer à programmer. On consultera plutot le manuel Débuter en calcul formel ou les autres manuels (menu Aide) pour apprendre à utiliser les fonctionnalités de Xcas en calcul formel, géométrie, tableur, etc..
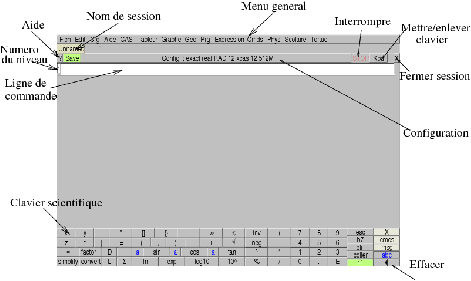
L’interface apparaît comme suit au lancement de Xcas. 2mm

Vous pouvez la redimensionner. De haut en bas cette interface fait apparaître :
Fich, Edit,
Cfg, Aide, CAS,
Tableur, Graphe, Geo,…
?
pour ouvrir l’index de l’aide
un bouton Save pour sauvegarder la session,
un bouton Config: exact real ... affichant la configuration
et permettant de la modifier,
un bouton STOP permettant d’interrompre un calcul trop long,
un bouton Kbd pour faire apparaitre un clavier ressemblant à celui d’une calculatrice,
qui peut faciliter vos saisies, et un bouton x pour fermer la session
1+1, suivi de la touche
"Entrée" ("Enter" ou "Return" selon les claviers).
Le résultat apparaît au-dessous, et une nouvelle ligne de commande
s’ouvre, numérotée 2.
Vous pouvez modifier l’aspect de l’interface et sauvegarder vos
modifications pour les utilisations futures (menu Cfg).
2mm
Vous n’avez pour l’instant qu’à
entrer des commandes dans les lignes de commandes successives.
Si vous utilisez la
version html de ce cours, vous pouvez copier-coller les commandes
proposées depuis votre navigateur.
Chaque ligne de commande saisie est exécutée par la
touche "Entrée". Essayez par exemple d’exécuter les
commandes suivantes.
1/3+1/4 sqrt(2)^5 resoudre(x+3=1,x) 50!
Toutes les commandes sont gardées en mémoire. Vous pouvez donc remonter dans l’historique de votre session pour modifier des commandes antérieures. Essayez par exemple de changer les commandes précédentes en :
1/3+3/4 sqrt(5)^2 resoudre(2*x+3=0) 500!
Notez que
Edit vous permet de préparer des sessions plus
élaborées qu’une simple succession de commandes. Vous pouvez
créer des groupes de lignes de commandes (sections),
ajouter des commentaires ou fusionner des niveaux en un seul niveau.
Prg contient la plupart des instructions utiles
pour programmer.
Les commandes de Xcas sont regroupées par thèmes dans les
menus du bandeau gris supérieur : CAS, Graphic,
Geo, Cmds, Phys, …
Lorsqu’on sélectionne une commande dans un menu,
CAS). Cliquez sur le bouton
Details pour afficher la page du manuel correspondant à la commande
dans votre navigateur.
Graphic)
? en haut à gauche,
ou faites afficher la zone de Messages (en utilisant le menu Cfg,).
Vous pouvez aussi configurer Xcas (menu Cfg puis Configuration generale
puis cocher la case Aide HTML automatique)
pour que la page correspondante du manuel
s’ouvre automatiquement dans votre navigateur.
Le menu Aide contient les différentes formes d’aide possible :
un guide de l’utilisateur (interface), un guide de référence
(Manuels->Calcul formel, aide detaillée sur chaque commande),
un Index (liste des commandes classées par ordre
alphabétique avec une ligne d’entrée permettant de se déplacer
facilement) et une recherche par mots clefs.
Si vous connaissez déjà le nom d’une commande et que vous désirez
vérifier sa syntaxe (par exemple factor), vous pouvez
saisir le début du nom de commande
(disons fact)
puis taper sur la touche de tabulation
(située à gauche de la touche A sur un clavier
français) ou cliquer sur le bouton ? en haut à gauche.
L’index des commandes apparaît alors dans une fenêtre, positionné
à la première complétion possible, avec une aide succinte sur chaque
commande.
Par exemple, vous voulez factoriser un polynôme, vous supposez que le nom de
commande commence par fact, vous tapez donc fact puis
la touche de tabulation, vous sélectionnez à la souris
factor (ou un des exemples) puis vous cliquez sur OK.
Vous pouvez aussi saisir ?factor pour avoir l’aide succinte
en réponse. Si le nom que vous avez saisi n’est pas reconnu, des
commandes proches vous sont suggérées.
Les nombres peuvent être exacts ou approchés.
Les nombres exacts sont les constantes prédéfinies, les entiers,
les fractions d’entiers et plus généralement toute expression
ne contenant que des entiers et des constantes, comme
sqrt(2)*e^(i*pi/3).
Les nombres approchés sont notés avec la notation scientifique
standard : partie entière suivie du point de séparation
et partie fractionnaire (éventuellement
suivie de e et d’un exposant).
Par exemple, 2 est un entier exact,
2.0 est la version approchée du même
entier; 1/2 est un rationnel, 0.5
est la version approchée du même
rationnel.
Xcas peut gérer des nombres entiers en précision arbitraire :
essayez de taper 500! et comptez le nombre de chiffres
de la réponse.
On passe d’une valeur exacte à une valeur approchée par
evalf, on transforme une valeur approchée en un rationnel
exact par exact
Les calculs sont effectués en mode exact si tous les nombres qui
interviennent sont exacts. Ils sont effectués en mode approché si
un des nombres est approché. Ainsi
1.5+1 renvoie un nombre approché alors que 3/2+1
renvoie un nombre exact.
sqrt(2) evalf(sqrt(2)) sqrt(2)-evalf(sqrt(2)) exact(evalf(sqrt(2)))*10^9 exact(evalf(sqrt(2)*10^9))
Pour les nombres réels approchés, la précision par défaut est
proche de 14 chiffres significatifs (la précision relative est de 53
ou 45 bits pour les réels flottants normalisés selon les versions de Xcas).
Elle peut être augmentée, en
donnant le nombre de décimales désiré
comme second argument de evalf.
evalf(sqrt(2),50) evalf(pi,100)
On peut aussi changer la précision par défaut pour tous les
calculs en modifiant
la variable Digits.
Digits:=50 evalf(pi) evalf(exp(pi*sqrt(163)))
La lettre i est réservée à √−1 et ne peut être
réaffectée ; en particulier on ne peut pas l’utiliser comme indice
de boucle.
(1+2*i)^2 (1+2*i)/(1-2*i) e^(i*pi/3)
Xcas distingue l’infini non signé infinity (∞), de
+infinity (+∞) et de -infinity (−∞).
1/0; (1/0)^2; -(1/0)^2
2mm
| Constantes prédéfinies | |
pi | π≃ 3.14159265359 |
e | e≃ 2.71828182846 |
i | i=√−1 |
infinity | ∞ |
+infinity | +∞ |
-infinity | −∞ |
Une chaîne est parenthésée par des guillemets ("). Un caractère est une chaîne ayant un seul élément.
s:="azertyuiop" size(s) s[0]+s[3]+s[size(s)-1] concat(s[0],concat(s[3],s[size(s)-1])) head(s) tail(s) mid(s,3,2) l:=asc(s) ss:=char(l) string(123) expr(123) expr(0123)
2mm
| Chaînes | |
asc | chaîne->liste des codes ASCII |
char | liste des codes ASCII->chaîne |
size | nombre de caractères |
concat ou + | concaténation |
mid | morceau de chaîne |
head | premier caractère |
tail | chaîne sans le 1ier caractère |
string | nombre ou expression->chaîne |
expr | chaîne->nombre (base 10 ou 8) ou expression |
On dit qu’une variable est formelle si elle ne contient aucune valeur :
toutes les variables sont formelles tant qu’elles n’ont pas été
affectées (à une valeur).
L’affectation est notée :=. Au début
de la session a
est formelle, elle devient affectée après l’instruction
a:=3, a sera alors remplacé par 3 dans tous
les calculs qui suivent, et a+1 renverra 4.
Xcas conserve tout le contenu de votre session. Si vous voulez que la variable
a après l’avoir affectée, soit à nouveau une variable formelle, il
faut la "vider" par purge(a). Dans les exemples qui suivent, les
variables utilisées sont supposées avoir été purgées avant chaque
suite de commandes.
2mmIl ne faut pas confondre
:= qui désigne l’affectation
== qui désigne une égalité
booléenne : c’est une opération binaire qui retourne 1 ou 0 (1 pour true
qui veut dire Vrai et 0 pour false qui veut dire Faux)
= utilisé pour définir une équation.
a==b a:=b a==b solve(a=b,a) solve(2*a=b+1,a)
On peut faire certains types d’hypothèses sur une variable avec
la commande assume, par exemple assume(a>2). Une
hypothèse est une forme spéciale d’affectation, elle efface
une éventuelle valeur précédemment affectée à la variable.
Lors d’un calcul, la variable n’est pas remplacée mais
l’hypothèse sera utilisée dans la mesure du possible, par exemple
abs(a) renverra a si on fait l’hypothèse a>2.
sqrt(a^2) assume(a<0) sqrt(a^2) assume(n,integer) sin(n*pi)
La fonction subst permet de remplacer une variable dans une
expression par un nombre ou une autre expression,
sans affecter cette variable.
subst(a^2+1,a=1) subst(a^2+1,a=sqrt(b-1)) a^2+1
Remarque : pour stocker une valeur dans une variable par référence,
par exemple pour modifier une valeur dans une liste (un vecteur, une
matrice), sans recréer une nouvelle liste mais en modifiant
en place la liste existante, on utilise l’instruction =<
au lieu de :=.
Cette instruction est plus rapide que l’instruction :=, car
elle économise le temps de copie de la liste.
Une expression est une combinaison de nombres et de variables
reliés entre eux par des opérations : par exemple
x^2+2*x+c.
Lorsqu’on valide une commande, Xcas remplace les variables par leur valeur si elles en ont une, et exécute les opérations.
(a-2)*x^2+a*x+1 a:=2 (a-2)*x^2+a*x+1
Certaines opérations de simplification sont exécutées automatiquement lors d’une évaluation :
Nous verrons dans la section 3.4.2 comment obtenir plus de simplifications.
En-dehors des règles de la section précédente, il n’y a pas de simplification systématique. Il y a deux raisons à cela. La première est que les simplifications non triviales sont parfois coûteuses en temps, et le choix d’en faire ou non est laissé à l’utilisateur ; la deuxième est qu’il y a en général plusieurs manières de simplifier une même expression, selon l’usage que l’on veut en faire. Les principales commandes pour transformer une expression sont les suivantes :
expand : développe une expression en tenant compte
uniquement de la distributivité de la multiplication sur l’addition et
du développement des puissances entières.
normal et ratnormal :
d’un bon rapport temps d’exécution-simplification, elles
écrivent une fraction rationnelle (rapport de deux polynômes)
sous forme de fraction irréductible développée; normal
tient compte des nombres algébriques (par exemple comme sqrt(2))
mais pas ratnormal. Les deux ne tiennent pas compte des relations
entre fonctions transcendantes (par exemple comme sin et cos).
factor : un peu plus lente que les précédentes, elle
écrit une fraction sous forme irréductible factorisée.
simplify : elle essaie de se ramener à
des variables algébriquement indépendantes avant d’appliquer
normal. Ceci est plus coûteux en temps et "aveugle" (on
ne contrôle pas les réécritures intermédiaires).
Les simplifications faisant intervenir des extensions
algébriques (par exemple des racines carrées)
nécessitent parfois deux appels et/ou des hypothèses (assume)
pour enlever des valeurs absolues avant d’obtenir la simplification
souhaitée.
tsimplify essaie de se ramener à des variables
algébriquement indépendantes mais sans appliquer normal
ensuite.
Dans le menu Math du bandeau supérieur, les 4 sous-menus
de réécriture
contiennent d’autres fonctions, pour des
transformations plus ou
moins spécialisées.
b:=sqrt(1-a^2)/sqrt(1-a) ratnormal(b) normal(b) tsimplify(b) simplify(b) simplify(simplify(b)) assume(a<1) simplify(b) simplify(simplify(b))
La fonction convert permet de passer d’une expression à une
autre équivalente, sous un format qui est spécifié par le
deuxième argument.
convert(exp(i*x),sincos) convert(1/(x^4-1),partfrac) convert(series(sin(x),x=0,6),polynom)
2mm
| Transformations | |
simplify | simplifier |
tsimplify | simplifier (moins puissant) |
normal | forme normale |
ratnormal | forme normale (moins puissant) |
expand | développer |
factor | factoriser |
assume | rajout d’hypothèses |
convert | transformer en un format spécifié |
De nombreuses fonctions sont déjà définies dans Xcas, en
particulier les fonctions classiques. Les plus courantes figurent dans
le tableau ci-après; pour les autres, voir le menu Math.
2mm
| Fonctions classiques | |
abs | valeur absolue |
round | arrondi |
floor | partie entière (plus grand entier ≤) |
ceil | plus petit entier ≥ |
abs | module |
arg | argument |
conj | conjugué |
sqrt | racine carrée |
exp | exponentielle |
log | logarithme naturel |
ln | logarithme naturel |
log10 | logarithme en base 10 |
sin | sinus |
cos | cosinus |
tan | tangente |
asin | arc sinus |
acos | arc cosinus |
atan | arc tangente |
sinh | sinus hyperbolique |
cosh | cosinus hyperbolique |
tanh | tangente hyperbolique |
asinh | argument sinus hyperbolique |
acosh | argument cosinus hyperbolique |
atanh | argument tangente hyperbolique |
Pour créer une nouvelle fonction, il faut la déclarer à l’aide
d’une expression contenant la variable.
Par exemple l’expression x2−1 est
définie par x^2-1. Pour la transformer en la fonction f qui
à x associe x2−1, trois possibilités existent :
f(x):= x^2-1 f:=x->x^2-1 f:=unapply(x^2-1,x) f(2); f(a^2)
On peut définir des fonctions de plusieurs variables à valeurs dans
ℝ comme f(x,y):=x+2*y et des fonctions de plusieurs
variables à valeurs dans ℝp
par exemple f(x,y):=(x+2*y,x-y)
Si f est une fonction d’une variable et E est une
expression, f(E) est une autre expression.
Il est essentiel de ne pas confondre fonction et expression.
Si on définit : E:=x^2-1, alors la variable E
contient l’expression x2−1. Pour avoir la valeur de cette
expression en x=2 il faut
écrire subst(E,x=2) et non E(2)
car E n’est pas une fonction.
Lorsqu’on définit une fonction,
le membre de droite de l’affectation n’est pas évalué.
Ainsi l’écriture E:=x^2-1; f(x):=E
définit la fonction f: x ↦ E car E n’est pas évalué.
Par contre E:= x^2-1; f:=unapply(E,x) définit bien la
fonction f: x↦ x2−1 car E est évalué.
Le signe ' après une expression permet de calculer la dérivée d’une
expression ou d’une fonction par rapport à la variable x. On
l’utilisera si possible. Si on veut dériver par rapport
à une autre variable ou plusieurs fois ou par rapport
à plusieurs variables, on utilise la commande diff qui
s’applique á une expression. Pour
dériver une fonction f,
on peut appliquer diff à l’expression f(x), mais alors le
résultat est une expression. Si on souhaite définir la fonction
dérivée, il faut utiliser function_diff.
E:=x^2-1 E' diff(E) f:=unapply(E,x) f' f'(2); f'(x) diff(f(x)) f1:=function_diff(f)
Il ne faut pas définir la fonction dérivée par
f1(x):=diff(f(x)), car x aurait dans cette définition
deux sens incompatibles : c’est d’une part la
variable formelle de dérivation et d’autre part l’argument
de la fonction f1. D’autre part, cette définition
évaluerait diff à chaque appel de la fonction (car
le membre de droite d’une affectation n’est jamais évalué), ce
qui serait inefficace. Il faut donc soit utiliser
f1:=function_diff(f),
soit f1:=unapply(diff(f(x)),x).
On peut ajouter et multiplier des fonctions,
par exemple f:=sin*exp. Pour composer des fonctions, on utilise
l’opérateur @ et pour composer plusieurs fois une fonction
avec elle-même, on utilise l’opérateur @@.
f:=x->x^2-1 f1:=f@sin f2:=f@f f3:=f@@3 f1(a) f2(a) f3(a)
Xcas distingue plusieurs sortes de collections d’objets, séparés par des virgules :
liste:=[1,2,4,2]
sequence:=(1,2,4,2)
ensemble:=%{1,2,4,2%}
Les listes peuvent contenir des listes (c’est le cas des matrices), alors que les séquences sont plates (un élément d’une séquence ne peut pas être une séquence). Dans un ensemble, l’ordre n’a pas d’importance et chaque objet est unique. Il existe une autre structure, appelée table, dont nous reparlerons plus loin.
Il suffit de mettre une séquence entre crochets pour en faire une liste
ou entre accolades précédées de % pour en faire un ensemble.
On passe d’une liste à sa séquence associée par op,
d’une séquence à sa liste associée en la mettant entre crochets
ou avec la fonction nop.
Le nombre d’éléments d’une liste est donné par size
(ou nops).
se:=(1,2,4,2)
li:=[se]
op(li)
nop(se)
nops(se)
%{se%}
size([se])
size(%{se%})
Pour fabriquer une liste ou une séquence, on utilise des commandes d’itération comme $ ou (qui itèrent une expression) ou (qui définit une liste à l’aide d’une fonction).
1$5 k^2 $ (k=-2..2) seq(k^2,k=-2..2) seq(k^2,k,-2..2) [k^2$(k=-2..2)] seq(k^2,k,-2,2) seq(k^2,k,-2,2,2) makelist(x->x^2,-2,2) seq(k^2,k,-2,2,2) makelist(x->x^2,-2,2,2)
La séquence vide est notée NULL, la liste vide
[]. Pour ajouter un élément à une séquence il suffit
d’écrire la séquence et ’élément séparés par une virgule.
Pour ajouter un
élément à une liste on utilise append.
On accède à un élément d’une liste ou d’une séquence grâce
à son indice mis entre
crochets, le premier élément étant d’indice 0 (on peut aussi
indicier
en commencant à 1 en utilisant des
parenthèses au lieu de crochets, mais attention au cas d’ambiguité avec
la définition d’une fonction
si on modifie un élément d’une liste)
se:=NULL; se:=se,k^2$(k=-2..2); se:=se,1 li:=[1,2]; (li:=append(li,k^2))$(k=-2..2) li[0],li[1],li[2]
Les polynômes sont souvent définis par une expression, mais
ils peuvent aussi être représentés
par la liste de leurs coefficients par ordre
de degré décroissant, avec comme délimiteurs poly1[ et ].
Il existe aussi une représentation
pour les polynômes à plusieurs variables. Les fonctions
symb2poly et poly2symb permettent
de passer de la représentation expression à la représentation
par liste et inversement,
le deuxième argument détermine s’il s’agit de polynômes
en une variable (on met le nom de la variable) ou de
polynômes à plusieurs variables (on met la liste des variables).
2mm
| Séquences et listes | |
| E$(k=n..m) | créer une séquence |
seq(E,k=n..m) | créer une séquence |
| [E$(k=n..m)] | créer une liste |
makelist(f,k,n,m,p) | créer une liste |
op(li) | passer de liste à séquence |
nop(se) | passer de séquence à liste |
nops(li) | nombre d’éléments |
size(li) | nombre d’éléments |
sum | somme des éléments |
product | produit des éléments |
cumSum | sommes cumulées des éléments |
apply(f,li) | appliquer une fonction à une liste |
map(li,f) | appliquer une fonction à une liste |
poly2symb | polynôme associé à une liste |
symb2poly | coefficients d’un polynôme |
Les instructions les plus souvent utilisées sont dans le menu CAS
(calcul différentiel, simplification, arithmétique, etc.).
Le menu Cmds contient d’autres instructions, en particulier
tout ce qui est relatif à l’algèbre linéaire.
Pour générer un graphe de fonction, surface,
etc. vous
pouvez utiliser les assistants du menu Graphe. Pour
les suites récurrentes, créez auparavant un niveau
de géométrie 2-d (menu Figure).
Vous pouvez aussi créer des objets géométriques, en utilisant
les instructions du menu Geo,
par exemple point(1,2) affiche le point de coordonnées
1 et 2, droite(A,B) la droite passant par deux points A et
B définis auparavant.
On peut donner des attributs graphiques aux objets graphiques
en ajoutant à la fin de l’instruction ayant un résultat graphique
l’argument affichage=... dont la
saisie est facilitée par le menu Graphe->Attributs.
Lorsqu’une ligne de commande contient une instruction graphique, le résultat est affiché dans un repère 2-d ou 3-d selon la nature de l’objet généré. On peut controler le repère avec les boutons situés à droite du graphique, par exemple orthonormaliser avec le bouton _|_. Si une ligne de commande contient des instructions graphiques et non graphiques, c’est la nature de la dernière instruction qui décide du type d’affichage.
L’instruction A:=click() permet de
définir une variable contenant l’affixe d’un
point du plan que l’on clique
avec la souris.
Le principal problème du calcul formel est la complexité des
calculs intermédiaires. Elle se traduit à la fois par le temps
nécessaire à l’exécution des commandes et par la place mémoire
requise. Les algorithmes implémentés dans les fonctions
de Xcas sont performants, mais ils ne
peuvent pas être optimaux dans tous les cas. La fonction time
permet de connaître le temps d’exécution d’une commande (si ce temps
est très court, Xcas exécute plusieurs fois la commande pour
afficher un résultat plus précis). La mémoire utilisée
apparaît dans les versions Unix dans la ligne d’état
(en rouge à bas à gauche). Si le temps d’exécution d’une
commande dépasse quelques secondes, il est possible que vous ayez
commis une erreur de saisie. N’hésitez pas à interrompre
l’exécution (bouton orange stop en bas à droite, il est
conseillé de faire une sauvegarde de votre session auparavant).
Comme le texte définissant un programme ne tient en général pas
sur une ou deux lignes, il est commode d’utiliser un éditeur
de programmes. Pour cela, on utilise
le menu Prg->Nouveau programme de Xcas. Les boutons
assistants Fonctions, Test, Boucle et le menu
Prg->Ajouter
facilitent la saisie des principales structures de controle
de programmation.
On peut tester l’égalité de 2 expressions en utilisant l’instruction
==, alors que != teste si 2 expressions ne sont pas
égales. On peut aussi tester l’ordre entre 2 expressions
avec <, <=, >, >=, il s’agit
de l’ordre habituel sur les réels pour des données numériques
ou de l’ordre lexicographique pour les chaines de caractères.
Un test renvoie 1 s’il est vrai, 0 s’il est faux. On peut combiner
le résultat de deux tests au moyen des opérateurs logiques &&
(et logique), || (ou logique) et on peut calculer la négation logique
d’un résultat de test ! (négation logique).
On utilise ensuite
souvent la valeur du test pour exécuter une instruction
conditionnelle si ... alors ... sinon ... fsi.
N.B. : Xcas admet aussi une syntaxe compatible avec le langage C
if (condition) { bloc_vrai } else { bloc_faux }.
Par exemple, on pourrait stocker la valeur absolue d’un réel x dans y par :
si x>0 alors y:=x; sinon y:=-x; fsi;
(on peut bien sur utiliser directement y:=abs(x)).
Exemples : Tester si un triangle dont on fait cliquer les 3 sommets à l’utilisateur est rectangle.
On peut exécuter des instructions plusieurs fois de suite en utilisant une boucle définie (le nombre d’exécutions est fixé au début) ou indéfinie (le nombre d’exécutions n’est pas connu). On utilise en général une variable de controle (indice de boucle ou variable de terminaison).
for(init;condition;incrementation){ instructions }for ... from ... to ... do ... odf:=1; for (j:=1;j<=10;j++){ f:=f*j; }f:=1; for j from 1 to 10 do f:=f*j; od;i comme indice
de boucle, car i est prédéfini (comme √−1)
while (...) { ... }while (b!=0){ r:=irem(a,b); a:=b; b:=r;}
Xcas accepte aussi l’arrêt de boucle en cours d’exécution
(if (...) break;) dont
l’usage peut éviter l’utilisation de variables de controle
compliquées.
La plupart des fonctions ne peuvent avoir une définition par une formule algébrique. On doit souvent calculer des données
intermédiaires, faire des tests et des boucles. Il faut alors définir
la fonction par une suite d’instructions, délimitées par { ... }.
La valeur calculée par la fonction est alors la valeur calculée
par la dernière instruction ou peut être explicitée en utilisant le
mot-clef return suivi de la valeur à renvoyer (N.B.: l’exécution
de return met un terme à la fonction même s’il y a encore
des instructions après).
Pour éviter que les données intermédiaires n’interfèrent
avec les variables de la session principale,
on utilise un type spécial de variables,
les variables locales, dont la valeur ne peut être modifiée ou accédée
qu’à l’intérieur de la fonction. On utilise à cet effet le mot-clef
local suivi par les noms des variables locales séparés par
des virgules.
Si une fonction calcule plusieurs données on peut les renvoyer dans
une liste.
Exemple : le PGCD
pgcd(a,b):={
local r;
while (b!=0){
r:=irem(a,b);
a:=b;
b:=r;
}
return a;
}
On clique ensuite sur le bouton OK, si tout va bien, le programme
pgcd est défini et on peut le tester dans une ligne de commande
par exemple par pgcd(25,15).
Dans la section suivante, on va voir comment exécuter en mode pas à pas un programme, ce qui peut servir à comprendre le déroulement d’un algorithme, mais aussi à corriger un programme erroné.
La commande debug permet de lancer un programme en mode d’exécution pas à pas. Elle ouvre une fenêtre permettant de diriger l’exécution du programme passé en argument. Par exemple, on entre le programme :
carres(n):={
local j,k;
k:=0;
for (j:=1;j<n+1;j++) {
k:=k+j^2;
}
return k;
}:;
On tape pour debugger le programme carres ci-dessus :
cela ouvre la fenêtre du debugger. En cliquant sur le bouton sst on peut exécuter pas à pas le programme en visualisant l’évolution des valeurs des variables locales et des paramètres du programme. Cela permet de détecter la grande majorité des erreurs qui font qu’un programme ne fait pas ce que l’on souhaite. Pour des programmes plus longs, le debugger permet de controler assez finement l’exécution du programme en placant par exemple des points d’arrêt.
Exercice : exécuter en mode pas à pas le programme pgcd
pour quelques valeurs des arguments.
|
| , |
| , eiπ/6, 4atan( |
| )−atan( |
| ) |
| x8−3x7−25x6+99x5+60x4−756x3+1328x2−960x+256 |
| x6−2x3+1, (−y+x)z2−xy2+x2y |
| ∫ |
| dx, | ∫ |
| ln(ln(x)) dx, | ∫ | ex2 dx, | ∫ | xsin(x)ex dx |
| ∫ |
|
| , | ∫ |
|
| dx |
| k, |
| k2, |
|
|
| ln(1+x+x2), |
| , | √ |
| , |
|
| ⎧ ⎪ ⎨ ⎪ ⎩ |
|
| A= | ⎛ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎠ |
On souhaite étudier des suites récurrentes (un) définies par un+1=f(un) et u0, où f est une fonction de ℝ dans ℝ, par exemple f(x)=√2+x.
Exercice 1
A1 par =sqrt(2+A0), puis déplacer la souris vers la partie situé en bas
à droite de la cellule A1 (le curseur souris change de forme), puis
appuyer sur le bouton de la souris et relâcher à la fin de la zone
où vous voulez copier la formule définissant A1.
La feuille de calcul précédente donne une idée de la convergence de la suite, mais ne donne aucune information quantitative sur la vitesse de convergence. Au lieu de calculer un nombre fixé de termes de la suite, on va écrire un programme avec un test d’arrêt selon la valeur |un+1−un| comparé à un nombre positif (petit) ε fixé à l’avance. Pour éviter que le programme ne boucle indéfiniment lorsque la suite ne converge pas (ou converge trop lentement pour la machine), on fixe aussi un nombre maximal d’itération N.
Exercice 2
Écrire un programme iter prenant en argument
la fonction f, la valeur de u0, de N et de ε, et
qui s’arrête dès que l’une des conditions suivantes est satisfaite :
Dans le premier cas le programme renverra la valeur de un+1, dans
le second cas une séquence composée de uN et de N.
Tester votre programme avec f(x)=√2+x et f(x)=x2.
On suppose que la fonction f satisfait aux hypothèses du théorème du point fixe. On notera k<1 la constante de contractance. On peut alors trouver un encadrement de la limite l de la suite (un) en fonction de un, un−1 et k.
Exercice 3
Écrire un programme iter_k prenant en argument
la fonction f, la valeur de u0, la constante k et l’écart toléré ε,
et qui s’arrête dès que | un − l | ≤ ε.
Vérifier les hypothèses du théorème du point fixe pour f(x)=2cos(x/3)
sur [0,2] et expliciter une constante de contractance k.
Déterminer une valeur approchée de la limite de (un)
à 1e-3 près en utilisant la fonction iter_k.
La convergence de ces suites est en général linéaire, le nombre de décimales exactes augmente de la même valeur à chaque itération. Par contre lorsqu’on est prêt d’une racine, la méthode de Newton permet en gros de multiplier par deux le nombre de décimales à chaque itération.
Exercice 4
| f(x)= |
|
iter, trouver un encadrement de
√7 à 1e-6 près par les deux méthodes (on pourra
prendre une valeur initiale approchée puis entière exacte pour avoir
une valeur numérique approchée puis une fraction).
Combien d’itérations sont nécessaires?
Dans certains cas, la fonction f n’est pas contractante, mais on peut réécrire l’équation à résoudre sous une autre forme avec une fonction contractante, par exemple en utilisant une fonction réciproque.
Exercice 5
Donner un encadrement à 1e-6 près d’une racine
de l’équation tan(x)=x sur l’intervalle ]3π/2,5π/2[ en
utilisant une méthode de point fixe. On observera qut tan n’est
pas contractante mais que sa fonction réciproque l’est (attention
à y ajuster correctement un multiple entier de π).
Digits:=30 (on pourra au préalable
mettre epsilon à 0 dans la configuration du CAS).
Même question sur votre calculatrice si vous en avez une.| F(x,y)= |
| y6 + x2 (11x2 y2−y6 −121y4−2) + |
| y8 + |
|
F(77617.0,33096.0)) et
l’autre en mode exact. Que pensez-vous de ces résultats?
Combien de chiffres significatifs faut-il pour obtenir un résultat
raisonnable en mode approché?time(a*(a+1))[0]) du produit
de a × (a+1) pour a=10n avec n=10000,20000,40000. Comment
évolue le temps de calcul lorsque le nombre de décimales double ?powmod et la méthode “prendre le reste modulo m après avoir
calculé an”
(vous pouvez aussi programmer la méthode rapide et la méthode
lente, cf. par exemple l’article exponentation rapide de wikipedia).| P(X) = an Xn + ... + a0 |
| P(X)−b0=(X−α )Q(X) |
| Q(X) = bn Xn−1 + ... +b2 X + b1 |
horn effectuant ce calcul:
on donnera en arguments le polynôme sous forme de la
liste de ces coefficients (dans l’exemple [1,0,-2,5]) et la
valeur de α et le programme renverra P(α ).
(On pourra aussi renvoyer les coefficients de Q).
Exercice 1.
Donner une majoration indépendante de x de l’erreur commise.
(A titre d’illustration, tracer la différence T7(x)−sin(x).)
Exercice 2.
On veut approcher cos(x) à 1e-6 près
en utilisant des développements en séries entières.
| T2k(x)= |
| (−1)j |
|
1e-6 de cos(x) sur [−100,100]
en justifiant et en effectuant les
étapes suivantes:
Exercice 3
| α− |
| + |
| − |
| ≤ arctan(α) ≤ α− |
| + |
|
1e-8 près de π/4= arctan(1).
| = 4 arctan( |
| ) − arctan( |
| ) |
Exercice 4
| g(x)= |
|
| I= | ∫ |
| g(x) dx |
Exercice 5
Cet exercice reprend les calculs de ln(x) et exp(x) discutés en cours
dans l’objectif de les illustrer par vos propres expériences sur ordinateur.
On considère ensuite la série ln2 = ∑k=0∞2/(2k+1) 32k+1. Jusqu’à quel rang faut-il aller afin de garantir une approximation à 10−5 près? Calculer cette approximation de ln2 avec Xcas. Même question pour 10−10. Conclusion?
Jusqu’à quel rang faut-il aller afin de garantir une approximation à 10−20 près? Calculer cette approximation de exp(−32) avec Xcas, d’abord en utilisant la précision standard de 53 bits, soit 16 décimales. Quel problème observez-vous? On pourra augmenter la précision des nombres flottants utilisés: quelle précision est nécessaire, environ, pour raisonnablement effectuer ce calcul?
Est-ce que ces problèmes se posent pour l’approximation de a0 = exp(−1)? Comment en déduire une approximation de exp(−32) avec un minimum d’opérations?
Exercice 6
On reprend des idées des exercices 4 et 5 pour implémenter le
calcul de la fonction
sinus intégral définie par :
| Si(x)= | ∫ |
|
| dt |
| ∫ |
|
| dt = |
|
Exercice 1
Donner le détail des calculs avec Bézout de la décomposition
en éléments simples de :
| f(x)= |
|
en déduire :
Exercice 2
Factoriser en mode réel et complexe
le polynôme
P(x)=x6+x4+x3+x2+x+1. Quels sont les degrés des facteurs ?
Même question mais en remplacant P par evalf(P).
En regroupant les racines de P, retrouver la factorisation exacte
de P dans ℝ et ℂ.
Exercice 3
Trouver une racine du polynôme P ci-dessus en appliquant
la méthode de Newton avec une valeur initiale complexe aléatoire,
éliminer cette racine par division
euclidienne, chercher une autre racine, etc. jusqu’à obtenir
la factorisation complète de P. Comparer la valeur de P
et celle obtenue en développant le produit des X−racine.
Bonus :
Écrire une fonction qui cherche une racine d’un polynôme
en utilisant la méthode de Newton. Ajouter un test pour
être sûr que la racine du polynôme est simple.
Tester avec le polynôme P ci-dessus.
Bonus : modifier la fonction ci-dessus pour trouver toutes
les racines (lorsqu’on trouve une racine, on divise le polynôme
par X−α, et on relance la recherche de racines sur le
polynôme obtenu).
Exercice 4
Écrire une fonction qui détermine les racines rationnelles
d’un polynôme P à coefficients entiers (elles sont
de la forme p/q où q divise le coefficient
dominant de P et ± p divise son coefficient de plus bas degré).
Tester avec le polynôme P=12x5+10x4−6x3+11x2−x−6.
Exercice 5
En utilisant les suites de Sturm, déterminer le nombre
de racines du polynôme P ci-dessus sur l’intervalle
[−3,0]. Même question sur ℝ tout entier.
Exercice 6
Représenter sur un même graphe cos(x) et
son polynôme interpolateur de Lagrange
en utilisant les 7 points d’abscisses équidistantes {0,π/6,...,π}.
Donner une majoration de l’erreur entre ce polynome et la fonction
cos en un réel x, représenter graphiquement
cette erreur pour x ∈ [0,π]. Où l’erreur est-elle
la plus grande ?
Exercice supplémentaire
Écrire un programme calculant les coefficients du
polynôme d’interpolation de Lagrange par l’algorithme des
différences divisées.
Exercice 7
Éliminer successivement a et b
du système :
| ⎧ ⎪ ⎨ ⎪ ⎩ |
|
puis trouver les racines du polynôme en c, puis calculer les valeurs de b puis a correspondantes (en cherchant les racines du PGCD des 2 puis 3 équations en b puis a après remplacement de c puis b par leurs valeurs).
Exercice 1 : Calculer une valeur approchée de
| ∫ |
|
|
par la méthode des rectangles, du point milieu et des trapèzes
en utilisant un pas de 1/10 et de 1/100 (vous pouvez la fonction
plotarea ou utiliser le
tableur ou écrire un programme effectuant ce calcul avec comme arguments
la fonction, la borne inférieure, la borne supérieure et le nombre
de subdivision). Observez numériquement
la différence entre les valeurs obtenues et la valeur exacte de
l’intégrale.
Exercice 2
Calculer le polynôme interpolateur P de Lagrange de f(x)=1/1+x2
aux points d’abscisse j/4 pour j variant de 0 à 4.
Donner un majorant de la différence entre P et f en un point
x ∈ [0,1]. Représenter graphiquement ce majorant.
Calculer une majoration de l’erreur entre l’intégrale de f
et l’intégrale de P sur [0,1].
En déduire un encadrement de π/4.
Exercice 3
On reprend le calcul de ∫01 dx/1+x mais en utilisant
un polynôme interpolateur de degré 4 sur N subdivisions de [0,1]
(de pas h=1/N). Déterminer une valeur de N telle que la valeur
approchée de l’intégrale ainsi calculée soit proche à 10−8 près
de ln(2). En déduire une valeur approchée à 10−8 de
ln(2).
Même question pour ∫01 dx/1+x2
et π/4 (pour majorer la dérivée n-ième de 1/1+x2,
on pourra utiliser une décomposition en éléments simples sur ℂ).
| D= | ⎛ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎠ |
| E= | ⎛ ⎜ ⎜ ⎜ ⎝ |
| ⎞ ⎟ ⎟ ⎟ ⎠ |
Ce document a été traduit de LATEX par HEVEA