Xcas/Khicas: calcul formel et algorithmique.

Bernard.Parisse@univ-grenoble-alpes.fr

2019

Table des matières

1  Introduction

Les nouveaux programmes de lycée ont introduit des nouveautés en algorithmique, avec l’accent mis sur la notion de fonction et l’utilisation de Python comme langage de programmation. Cela ne doit pas faire oublier que l’utilisation de logiciels de calcul numérique, calcul formel et représentation graphique conserve toute sa place dans les programmes de mathématiques : on lit dans le préambule des programmes de 1ere, Terminale
L’utilisation de logiciels (calculatrice ou ordinateur), d’outils de visualisation et de représentation, de calcul (numérique ou formel), de simulation, de programmation développe la possibilité d’expérimenter, favorise l’interaction entre l’observation et la démonstration et change profondément la nature de l’enseignement. L’utilisation régulière de ces outils peut intervenir selon trois modalités :

Ces deux dernières années, une bonne partie du développement de Xcas a eu pour objectif de couvrir l’ensemble de ces thèmes au sein du même logiciel, de l’algorithmique en langage naturel ou en syntaxe Python, du calcul numérique et formel et des représentations graphiques, et ce sur une grande variété de matériels: ordinateurs (et dans une moindre mesure tablettes ou smartphones), mais aussi calculatrices graphiques de milieu de gamme (Casio, Numworks) dont l’importance en milieu scolaire est grande en raison de leur souplesse d’utilisation. Le fichier que vous lisez transforme d’ailleurs votre navigateur en logiciel de calcul formel (vous pouvez taper une commande Xcas dans la ligne de commande en bas).

Dans la section 2, nous présentons les aspects calcul formel, la section 3 sera consacrée à l’algorithmique pour l’enseignement, nous y montrerons que Xcas peut être utilisé comme plateforme de programmation compatible Python au lycée, la section 4 présente plusieurs plateformes matérielles où on peut installer Xcas, en particulier calculatrices, avec leurs particularités et limites, la section 5 des liens pour installer.

N.B. : les commandes ci-dessous permettent de passer le moteur de calcul en mode de compatibilité Python et de désactiver l’utilisation des racines carrées dans les factorisations : 

python_compat(1):; with_sqrt(false):;

onload

2  Calcul formel

Le calcul formel est la première fonctionnalité implémentée dans Xcas, ainsi que ses interactions, en particulier la géométrie analytique exacte. Comme dans tout système de calcul formel, il est possible d’étendre le système en programmant de nouvelles commandes, avec le langage utilisateur (et même, pour les utilisateurs experts ayant besoin du maximum de vitesse, par des modules dynamiques écrits en langage compilé).

Le menu Outils de Xcas permet de trouver efficacement les commandes les plus utilisées, par thèmes : résolution d’équations et systèmes, calcul différentiel et intégral, simplifications, arithmétique, algèbre linéaire, probabilités. Un menu scolaire est destiné aux élèves de lycée. Les autres commandes sont dans le menu Cmds, ou Graphes. Un menu spécifique est prévu pour écrire des programmes (avec des assistants pour créer une fonction, un test ou une boucle), construire une figure de géométrie (2d/3d), ou saisir une matrice ou un tableur formel, ou créer une figure logo. Lorsqu’on sélectionne une commande depuis le menu, l’index de l’aide en ligne rapide apparait à cette commande, avec une description courte et des exemples qu’il suffit en général de recopier, modifier et exécuter. En cliquant sur le bouton Details, l’aide plus complète apparait dans une fenêtre du navigateur.
La prise en main est en général rapide, voici un exemple d’ énoncé de début de 1ère année de licence, parcours physique, en 1 heure les étudiants arrrivent à l’exercice 6, et un énoncé de 2ème année de licence, parcours physique, dont la partie TP de prise en main se fait en 1h30 environ. Les difficultés principales rencontrées sont le parenthésage (priorité des opérateurs, mais aussi absence de parenthèses après les fonctions trigonométriques) et l’utilisation de la multiplication implicite entre deux variables, par exemple entre ii et π\pi (ipi au lieu de i*pi), ou xy au lieu de x*y).

Dans l’enseignement, le calcul formel de Xcas peut servir d’outil de vérification. La vérification est un aspect souvent négligé par les élèves et étudiants ou alors ils s’en remettent à l’enseignant, sans tester par eux-mêmes avec d’autres approches (représentation graphique, essai pour des valeurs particulières de paramètres, calcul symbolique avec du calcul formel). Dans les cas trop techniques (“trop” dépend bien sur de l’élève), faire faire le calcul au logiciel peut permettre de comprendre des concepts qui seraient sinon noyés dans les difficultés rencontrées pour mener à bien les calculs à la main. Bien entendu, il faut continuer à faire du calcul mental et du calcul littéral à la main, mais il faut aussi savoir se servir d’un logiciel de calcul formel et l’utiliser à bon escient.

Un autre intérêt de Xcas est de permettre de faire des preuves assistées. Xcas peut servir, comme d’autres logiciels non formel, d’aide à la conjecture, que l’on démontre ensuite papier-crayon. De plus en géométrie analytique, on peut faire des calculs exacts et avec des paramètres, ce qui permet de fournir une preuve par le logiciel de certains théorèmes, preuve que l’on peut bien sur compléter par une preuve à la main (en géométrie synthétique par exemple). Enfin, on peut se servir de Xcas comme d’une boule de cristal. Par exemple si on souhaite déterminer les entiers a≥1a\geq 1 tels que a 4+4a^4+4 est premier, la factorisation de a 4+4a^4+4 est hors de portée d’un élève de lycée, mais il peut vérifier en développant à la main la factorisation calculée par le logiciel.

Cet exemple nous semble formateur, car il permet de manipuler ensuite plusieurs fois des identités remarquables pour terminer la résolution d’une part (il faut résoudre des équations auxiliaires, chaque facteur ci-dessus peut-il être 1 ?), et pour vérifier la factorisation renvoyée par le logiciel. Pendant l’étape de recherche, il se prête aussi à l’écriture d’un algorithme 

def listea(n):
  L=[]
  for a in range(n):
    p=a**4+4
    if isprime(p):
      L.append(a)
  return L

onload
et on peut amener une discussion avancée sur la notion de preuve assistée par logiciel

D’autres activités du même type sont en cours de développement par le groupe Preuve par le calcul formel de l’IREM de Grenoble.
Par exemple en seconde, on peut faire montrer au préalable avec l’aide du calcul formel que 1 plus la somme du produit de 4 entiers consécutifs est un carré parfait :



et laisser les élèves aborder de manière plus autonome la question des entiers premiers de la forme a 4+4a^4+4.
En terminale, lorsqu’on donne à prouver des relations par récurrence, une étape préalable est de deviner la formule. Mais ce n’est pas toujours évident, par exemple, pour : S n=∑ k=1 nk(n−k)S_n=\sum_{k=1}^n k(n-k) les premières valeurs de S nS_n ne sont pas très parlantes. 

S(n):=sum(k*(n-k),k,1,n):; [S(n) for n in range(10)]

onload
On peut alors faire le calcul de la somme à la machine de manière explicite



et ensuite la prouver par récurrence en donnant en indication de vérifier que : S n+1−S n=∑ k=1 nkS_{n+1}-S_n = \sum_{k=1}^n k

La géométrie analytique est un autre domaine d’utilisation possible de Xcas au lycée. Par exemple, on trace la courbe représentative de la fonction exponentielle et de son inverse, les tangentes au point d’abscisses aa se coupent orthogonalement et les points d’intersection de ces tangentes avec l’axe des abscisses sont à distance fixe (2).

=
Not evaled



On observe que le paramètre aa prend une valeur numérique approchée pour les affichages mais pas pour les calculs exacts. On a donc une preuve formelle des résultats. On peut ensuite revenir sur la justification de l’orthogonalité par un calcul mental immédiat sur les pentes


Pour la distance, on peut faire la différence entre les deux équations de droite écrites sous la forme x−x 0=1f′(x 0)(y−y 0)x-x_0=\frac{1}{f'(x_0)}(y-y_0)

3  Algorithmique et programmation

Comprendre un algorithme, c’est souvent difficile, le programmer, c’est à la fois plus difficile mais aussi source de satisfaction quand on a écrit un programme qui fonctionne, ce qui peut motiver des élèves par ailleurs peu intéressés par les maths.

Enseigner l’algorithmique et la programmation est d’autant plus délicat si on n’est pas soi-même à l’aise et qu’on ne dispose pas d’une formation permanente à la hauteur de l’enjeu. On risque de déclarer faux un algorithme correct, et surtout on risque de se trouver en situation de grand stress pendant une séance de TP si on n’arrive pas à débloquer rapidement des élèves devant une erreur de syntaxe ou d’exécution (en général on se retrouve devant une dizaine de “M’sieur ça marche pas”, puis tous les élèves se démotivent). Avoir des objectifs trop ambitieux, c’est courir le risque de voir se reproduire ce qui s’est passé avec les maths modernes ou plus récemment les statistiques inférentielles. On risque de voir se multiplier des séances de bachotage où l’enseignant écrit en début de séance un programme tout fait au tableau, que les élèves sont invités à recopier religieusement, avec des formules rituelles mal comprises (par exemple from math import *).

Il importe donc de bien distinguer l’algorithme que l’on pourra traduire essentiellement dans tout langage de programmation et le programme avec les spécificités de syntaxe de Python (pas toujours heureuses). Il ne faut pas oublier que d’autres langages de programmation populaires existent aujourd’hui (par exemple Javascript) et que dans 10 ou 20 ans, un autre langage de programmation aura peut-etre supplanté Python chez les scientifiques qui l’utilisent aujourd’hui (le langage Julia par exemple). L’algorithme en langage naturel est beaucoup plus pérenne, il se prête aussi mieux à une analyse mathématique (y-a-t-il un invariant de boucle ? quel est le nombre d’itérations de cette boucle ? est-on bien sur que le programme se termine ?), c’est d’ailleurs en langage naturel que les algorithmes sont présentés dans les articles de recherche en calcul formel ou les références d’algorithmique, comme par exemple la référence en livre numérique pour l’algorithmique de l’agrégation interne. C’est enfin le langage qui se prête le mieux à une évaluation papier-crayon, comme c’est le cas actuellement au bac, espérons que cela ne changera pas (mais on peut le craindre en lisant les sujets 0 du bac 2020...).

Comme les programmes scolaires imposent Python comme langage de programmation, il faut bien sur utiliser une syntaxe compatible avec Python lorsqu’on écrit un programme, mais j’espère avoir convaincu qu’il ne faut pas être intégriste, utiliser Xcas en syntaxe compatible Python est tout à fait conforme aux programmes de maths et présente plusieurs avantages pour l’enseignement des mathématiques par rapport à un environement Python natif :

D’un point de vue progression, il me parait raisonnable d’avoir comme premier objectif, avant d’écrire une fonction, d’être capable d’écrire une ligne de commande de shell, pour maitriser un minimum les règles d’écriture (priorité de + et *, parenthésage, appel de fonctions usuelles). C’était indispensable sur les calculatrices auparavant, mais plus maintenant avec la généralisation de la saisie en écriture naturelle (ou 2d), sauter cette étape risque d’augmente la difficulté du passage à la programmation. On peut ici utiliser la calculatrice en passant en mode de saisie algébrique. Si on a un logiciel de calcul formel ou une calculatrice formelle cela peut motiver les élèves, car ils pourront vérifier des développements et factorisations.

On peut ensuite faire des définitions de fonction algébriques, par exemple le maximum en valeur absolue de 2 puis de 3 réels. 

def maxabs2(a,b):
    return max(abs(a),abs(b))
def maxabs3(a,b,c):
    return max(maxabs2(a,b),abs(c))

onload

Avec la tortue, on peut introduire la notion de suite d’intructions, puis de fonctions dans un contexte non algébrique. On peut commencer par faire tracer un carré instruction par instruction depuis le shell puis regrouper en un programme, 

def Carre():
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche

puis simplifier à l’aide d’une boucle1 

def Carre():
  for j in range(4):
    avance(20)
    tourne_gauche

onload

Puis on peut passer en paramètre la longueur, puis le nombre de cotés d’un polygone régulier 

def polyg1(l,n):
  for j in range(n):
     avance(l)
     tourne_gauche(360.0/n)

onload

et par exemple finir par construire tous les polygones réguliers de 3 à nn cotés :

#
efface
for j in range(3,15): 
  polyg1(20,j)


Une approche alternative consiste à travailler en géométrie analytique. On commence par définir deux points AA et BB. Puis on calcule les abscisses de AA et de BB, les ordonnées de AA et BB, les coordonnées du milieu de AA et BB, et on construit le point milieu. 

# construction du milieu de 2 points
A=point(1,3)
B=point(-2,2)
Ax=abscisse(A)
Bx=abscisse(B)
Ay=ordonnee(A)
By=ordonnee(B)
Mx=(Ax+Bx)/2
My=(Ay+By)/2
M=point(Mx,My)

onload
On passe alors à la définition de fonction prenant en argument les deux points AA et BB et renvoyant le point MM, milieu de AA et BB : 

def Milieu(A,B):
  Ax=abscisse(A)
  Bx=abscisse(B)
  Ay=ordonnee(A)
  By=ordonnee(B)
  Mx=(Ax+Bx)/2
  My=(Ay+By)/2
  return point(Mx,My)

onload

On peut aussi calculer l’équation de la droite ABAB, chercher l’intersection de deux droites, construire le centre du cercle circonscrit, etc. Le manuel Algorithmique au lycée de Xcas contient beaucoup d’exemples de ce type.

On peut ensuite passer à des squelettes de fonction plus ambitieuses à compléter par exemple pour la recherche de longueur approchée de courbe et du minimum d’une expression. Notre groupe IREM de Grenoble propose trois TP pour l’enseignement de l’algorithmique en seconde avec Xcas, écrits en langage naturel avec des traductions en Python. Le troisième énoncé recherche d’un extremum, illustre comment on peut proposer de faire modifier un programme existant, sans que les élèves ne perdent du temps à recopier un programme au tableau avec risques d’erreur de recopie.

4  Xcas/χ\chicas à la conquête du web et des calculatrices

4.1  Xcas et Xcas pour Firefox

Le moteur de calcul de Xcas, Giac, est utilisable par l’intermédiaire de nombreuses interfaces. La plus connue est le logiciel Xcas pour PC/Mac, mais Giac est aussi le moteur de calcul de la fenêtre de calcul formel de Geogebra. Xcas comme Geogebra regroupe en une seule interface plusieurs fonctionnalités : calcul formel, calcul numérique, géométrie dans le plan et l’espace, tableur ; Xcas met plus l’accent sur la programmation et la compatibilité Python (on peut programmer en Javascript dans Geogebra mais ce n’est pas aussi simple).

On peut aussi utiliser l’interface Xcas pour Firefox avec un navigateur compatible, donc depuis un PC/Mac, ou depuis une tablette ou un smartphone. Cette interface est moins complète (en particulier pas de tableur), mais permet d’échanger par un simple clic des sessions de travail (programme et historique de calculs) soit en privé par e-mail, soit en les publiant sur le forum de Xcas dans la section dédiée ou sur un autre forum. La personne qui reçoit une session de travail par mail clique sur le lien inclus, ce qui ouvre la session dans son navigateur, elle peut la modifier et renvoyer la session modifiée à l’expéditeur, on peut imaginer noter des compte-rendus de TP de cette manière. Enfin, il est possible d’exporter une session de travail Xcas pour l’importer sur une calculatrice Casio, plusieurs exemples de sessions sont disponibles sur cette page

4.2  χ\chicas: versions pour calculatrices

Historiquement, le premier portage de Xcas sur calculatrices a été fait pour les HP Prime (Giac en est le moteur de calcul formel),

Mais il s’agit d’un modèle haut de gamme (150 euros au lancement) très peu diffusé en France. Ensuite Xcas a été porté sur TI Nspire pour proposer de calcul formel sur les modèles non CAS dont le prix à l’époque était proche de 130 euros pour la Nspire au lieu de 170 pour la Nspire CAS (c’est à ce moment-là que le nom de χ\chicas a été adopté, en jouant sur l’écriture proche du X et du χ\chi et en pied de nez aux constructeurs qui font payer un supplément déraisonnable pour disposer de calcul formel).

Les calculatrices proposant du calcul formel (Casio Classpad, HP Prime, TI nspire CX CAS), sont peu répandues dans le secondaire, en raison de leur prix dépassant la barre psychologique des 100 euros (leur prix varie encore de 110 à 120 euros en cette rentrée 2019), elles sont essentiellement réservées aux élèves des milieux favorisés envisageant d’aller en prépas. Lorsque je fais un sondage dans mes amphis de licence le nombre d’étudiants ayant une calculatrice CAS se compte sur les doigts d’une main, c’est surement plus en classes prépas mais ca reste très minoritaire au lycée, on ne peut donc absolument pas accuser le calcul formel sur calculatrices d’être la cause des difficultés rencontrées par les étudiants en calcul littéral. Je pense que la vraie raison est la diminution du temps consacré à ces activités au lycée, en particulier en géométrie analytique, en raison de réductions de volumes horaire ou au profit d’autres thèmes (dont l’algorithmique).

Démocratiser un outil de vérification ou de calcul dans les cas techniques me parait donc important, et c’est la raison pour laquelle j’ai investi du temps de développement dans le portage de Xcas sur des calculatrices graphiques milieu de gamme, profitant du renouvellement de ces gammes par les constructeurs suite à l’introduction de Python :

Ces portages de Xcas sur calculatrices n’ont pas de tableur, mais ce n’est pas très grave puisque ces calculatrices ont leur propre tableur natif, sauf Numworks.
Notez que pour faire de l’algorithmique, χ\chicas est un environnement bien plus complet que le microPython proposé par les constructeurs de calculatrices, il offre un équivalent partiel des modules Python math+cmaths+random+ numpy+scipy+giacpy+ matplotlib+turtle+graphique pixelisé, alors que le MicroPython des constructeurs se limite à maths et random pour Casio et TI, pour Numworks, s’y ajoute cmaths, la tortue Python et un module graphique pixelisé, tout cela étant complètement isolé du reste de la calculatrice. Ainsi une fonction microPython ne peut pas être représentée graphiquement dans l’application fonction, contrairement à une fonction χ\chicas qui peut être représentée graphiquement comme les fonctions usuelles par une simple commande plot.
Par exemple, le calcul du prix d’un billet de train (au tarif kilométrique national) est une fonction affine par morceaux : 

def prix(km):
  if km<=16:
    return 0.7781+0.1944*km
  if km<=32:
    return 0.2503+0.2165*km
  if km<=64:
    return 2.0706+0.1597*km
  if km<=109:
    return 2.8891+0.1489*km
  if km<=149:
    return 4.0864+0.1425*km
  if km<=199:
    return 8.0871+0.1193*km
  return 7.7577+0.1209*km # if km<=300:

onload

il est intéressant de pouvoir la représenter graphiquement pour tester qu’on ne s’est pas trompé :

De même si on fait un programme de simulation, on souhaitera souvent faire une représentation graphique, typiquement un histogramme : 

# simule n tirages de pile ou face
# renvoie le nombre de piles
def simu1(n):
  s=0
  for j in range(n):
    if random()>0.5:
      s=s+1
  return s

# on fait 2000 experiences
l=[simu1(50) for j in range(2000)]
# on affiche l'histogramme
histogram(l)

onload

Concernant l’environnement, on dispose (pour le moment sur Casio et Numworks) d’un éditeur avec coloration syntaxique (ou soulignement sur les 35eii monochromes), affichage des numéros de ligne, fonction de copier/coller,

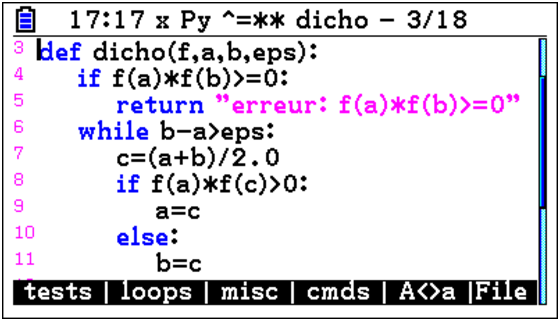
Le test de la syntaxe se fait directement depuis l’éditeur, en cas d’erreurs, le curseur est positionné à la ligne où la première erreur est détectée. De plus, il est possible d’exécuter un programme en mode pas à pas en voyant la valeur des variables évoluer, ce qui est très utile pour mettre au point un programme, mais est certainement aussi très utile pour comprendre ce qu’est une boucle, un test ou le déroulement d’un algorithme. Ainsi, le programme exemple de résolution d’une équation du second degré de la Numworks (où roots a été renommé en rac car roots est une commande Xcas) 

# rac(a,b,c) calcule les racines de a*x**2+b*x+c=0
def rac(a,b,c):
  delta = b*b-4*a*c
  if delta == 0:
    return -b/(2*a)
  elif delta > 0:
    x_1 = (-b-sqrt(delta))/(2*a)
    x_2 = (-b+sqrt(delta))/(2*a)
    return [x_1, x_2]
  else:
    return None

onload
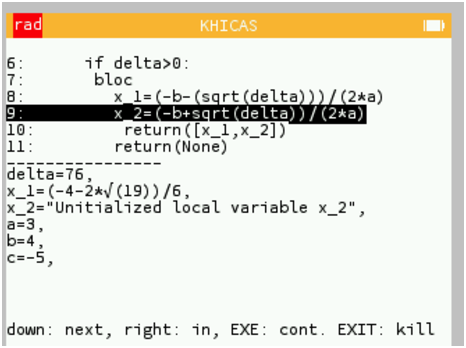
peut être exécuté en pas à pas par la commande debug(rac(3,4,-5)) dans le shell de l’application KhiCAS, après quelques étapes, on voit :

4.3  Plaidoyer contre la mise en place du mode examen actuel.

La DGESCO a annonce fin novembre 2019 que le mode examen serait mis en place en 2019/20. Ceci va empêcher les élèves possédant une Casio Graph 35eii ou une Casio Graph 90+e d’utiliser χ\chiCAS aux examens.

Plus généralement, c’est l’accès à l’ensemble de l’offre de logiciels développés par la communauté qui va être bloqué par cette mesure. L’apport des logiciels libres ou/et open-source à l’informatique est indéniable, ils ont permis l’essor d’Internet, ils sont au coeur du système d’exploitation de la majorité des smartphones... Le monde des calculatrices est très en retard sur ce point, ce qui permet aux constructeurs de segmenter le marché et de bénéficier d’une forte rentabilité au détriment des élèves. Alors que le monde des calculatrices s’ouvre lentement au libre, la mise en vigueur du mode examen va considérablement freiner cette ouverture. Cela va probablement aussi empêcher certains élèves de découvrir leurs talents en programmation : il y a beaucoup de programmeurs talentueux qui ont commencé par programmer sur leur calculatrice, car elle est à portée de main toute la journée (par exemple pendant les transports scolaires), moins complexe à maitriser qu’un ordinateur, et on peut facilement montrer ses créations à ses camarades. Mais c’est beaucoup moins motivant si on ne peut pas se servir de ses propres programmes en examen.

Ci-dessous un tableau de comparaison des calculatrices sur deux fonctionnalités importantes, la programmation en Python et le calcul formel, proposées par le constructeur ou par des applications programmées par des tiers.

calculatriceprix neuf ≈\approxPython constructeurCAS constructeurPython tiersCAS tiers
Casio Graph 35+USB55nonnonCasioPythonEigenmaths
Casio Graph 35eii65ouinon(constructeur)Eigenmaths, χ\chiCAS
Casio Graph 90+e80ouinon(constructeur)Eigenmaths, χ\chiCAS
Casio Classpad120nonouinon(constructeur)
TI8250nonnonnonnon
TI83CE Python80ouinon(constructeur)non
TI Nspire CX115nonnonNdless+MicroPythonNdless + χ\chiCAS
TI Nspire CX CAS120nonouiNdless+MicroPythonNdless + χ\chiCAS
Numworks80ouinon(constructeur)χ\chiCAS
HP Prime110-150partieloui(constructeur 2020?)(constructeur)

Au vu de ce tableau, il parait clair que le mode examen va renforcer les inégalités. Seuls les élèves pouvant se payer une calculatrice haut de gamme bénéficient du CAS du constructeur et ils devront acheter une autre calculatrice pour avoir MicroPython. Hors mode examen, la Casio Graph 35e permet pour 55 euros d’accéder aux deux fonctionnalités grâce à des programmes tiers (même si c’est partiel pour le CAS) et pour 65 euros on a Python et CAS, comme sur le haut de gamme. La Numworks fait un peu bande à part, l’ouverture relative de son code source permet pour l’instant de faire tourner χ\chiCAS en mode examen (mais ce n’est pas pour autant le modèle miracle, elle n’a pour l’instant pas de tableur et sa capacité mémoire est très faible).

Ce qu’on voit ici pour ces deux grandes fonctionnalités est également vrai pour d’autres fonctionnalités, les constructeurs ont intérêt à ne pas proposer certaines fonctionnalités sur les modèles bas ou milieu de gamme, même si c’est techniquement possible, pour inciter à acheter un modèle plus cher. Cette stratégie est confortée par le mode examen, qui empêche de compléter sa calculatrice avec des programmes tiers. J’ai contacté Casio Education à plusieurs reprises pour leur demander de mettre en place un processus permettant de valider en mode examen des addins écrits par des tiers, sans aucun effet pour le moment. On peut aussi observer que parmi les constructeurs, TI est le seul à ne pas disposer de CAS sur un modèle milieu de gamme hors mode examen, et ce en raison de leur politique de fermeture, TI a donc tout intérêt à ce que le mode examen soit mis en vigueur.

Aussi je m’interroge, l’existence de banques de données de sujets, qui semble le motif principal du retour en grâce du mode examen (malgré tous les inconvénients qui ont repoussé sa mise en application aux sessions 2018 et 2019 du bac), justifie-t-il que l’on aille à ce point à l’encontre du principe constitutionnel d’égalité entre les élèves ? De toutes façons, le principe des banques de sujet est à mon avis mauvais, car les sujets seront connus des professeurs à l’avance, il leur sera difficile de résister aux pressions qui vont s’exercer sur eux pour ne pas en tenir compte dans les séances qui précèderont le controle continu (et puis même sans pression des établissements et parents d’élèves, c’est tout simplement humain de donner un coup de pouce à ses élève au moyen d’un petit exercice de révision un peu ciblé).

Je plaide donc pour l’abrogation du mode examen actuel. On pourrait très bien organiser une partie des examens sans calculatrices (par exemple une heure sur quatre ou une évaluation sur 2 ou 3), et organiser le reste des évaluations avec calculatrices sans mode examen sur un sujet national commun à toute la France, ce serait bien plus équitable, et cela éviterait bien des problèmes (surveillance de la mise en place du mode examen en début d’épreuve, possibilité d’utiliser d’anciens modèles de calculatrices n’ayant pas le mode examen, ...). Et que dire des élèves de terminale qui sont placés devant le fait accompli d’un changement de conditions de passage du bac 2020 par rapport aux sessions précédentes au bout d’un tiers de l’année, alors que la réunion DGESCO-APMEP de juin 2019 laissait présager que le mode examen ne serait pas mis en vigueur. (“Qu’en est-il de l’usage de la calculatrice avec mode examen ? Réponse : Le mode examen est trop contraignant à valider dans les salles d’examen avec de nombreux candidats.”). Certains élèves modestes qui pensaient pouvoir passer le bac cette année avec la calculatrice graphique du grand frère ou de la grande soeur vont devoir composer avec une calculatrice collège ou se faire offrir une calculatrice conforme comme cadeau de Noël...

Si on tient absolument à conserver le mode examen, alors le cahier des charges devrait obliger les constructeurs à laisser fonctionner certaines applications tierces en mode examen, afin de ne pas trop défavoriser les élèves modestes. L’histoire a démontré que la régulation par la libre concurrence dans le domaine des calculatrices fonctionne mal : il y a un accord tacite des acteurs majeurs du secteur pour stratifier l’offre.

5  Ressources

6  Conclusion

La mise en vigueur du mode examen aux épreuves du bac va donc avoir comme conséquence l’augmentation de prix du modèle CAS le moins cher du marché au lycée : la Casio Graph 35eii (à moins de 65 euros) n’étant plus éligible (sauf si Casio décide de signer certains addins pour les autoriser en mode examen), c’est désormais la Numworks N0110 à 79 euros qui est la moins chère.

Le mode examen va freiner l’accès à un modèle de calculatrices pouvant faire du calcul formel. Ceci dit, même si le calcul formel est désactivé en mode examen, il reste utilisable en-dehors et permet aux élèves de vérifier des exercices chez eux ou d’explorer des maths en délégant les calculs techniques à la machine. Je pense donc que le nombre d’élèves équipés devrait augmenter à cette rentrée, d’une part avec ces portages de Xcas, d’autre part avec les solutions CAS des constructeurs (Casio, HP et TI) dont les prix ont baissé à cette rentrée.

Et pour ceux qui n’ont pas de calculatrice formelle, le calcul formel est accessible sur ordinateur, tablette voire même smartphone. Reste à faire le meilleur usage possible de cette nouvelle fonctionnalité, en l’intégrant intelligeamment à l’enseignement des maths, i.e. sans excès dans un sens ou dans l’autre (ne plus faire de calcul mental à un extrême ou interdire son usage à l’autre extrême).

  

1
Remarque de Patrice Debrabant : “A ce propos, je trouve qu’il y a des trucs embarrassants quand on utilise Python pour formuler des algorithmes. A commencer par la traduction en Python d’une simple boucle répéter 10 fois en ’for i in range(n):’. Il y a un glissement (de la répétition à l’itération Python), et accepter ce glissement comme s’il allait de soit me semble problématique.”.
Xcas permet d’utiliser la structure repete, qui donnerait
repete(4,avance(20),tourne_gauche) mais je ne l’ai pas utilisée ici, car Python n’a pas de structure équivalente.
Retour à la page principale de Giac/Xcas.