




suivant: Other functions
monter: Differential equations
précédent: Solving differential equations :
Table des matières
Index
Laplace transform and inverse Laplace transform : laplace ilaplace
laplace and ilaplace takes one, two or three arguments :
an expression and optionnaly the name(s) of the variable(s).
The expression is an expression of the current variable (here x) or an
expression of the variable given as second argument.
laplace returns the Laplace transform of the expression given as argument
and ilaplace the inverse Laplace transform of the expression given
as argument. The result of laplace and ilaplace is expressed
in terms of the variable given as third argument if supplied
or second argument if supplied or x otherwise.
Laplace transform (laplace) and inverse Laplace transform
(ilaplace) are useful to solve linear differential equations
with constant coefficients. For example :
y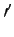
+
p.
y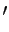
+
q.
y =
f (
x)
y(0) =
a,
y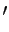
(0) =
b
Denoting by
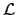 the Laplace transform,
the following relations hold :
the Laplace transform,
the following relations hold :
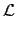 (y)(x) (y)(x) |
= |
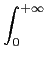 e-x.uy(u)du e-x.uy(u)du |
|
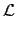 -1(g)(x) -1(g)(x) |
= |
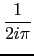 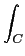 ez.xg(z)dz ez.xg(z)dz |
|
where C is a closed contour enclosing the poles of g.
Input :
laplace(sin(x))
The expression (here sin(x)) is an expression of the current variable
(here x) and the answer will also be an expression of the current variable
x.
Output :
1/((-x)^2+1)
Or input :
laplace(sin(t),t)
here the variable name is t and this name is also used in the answer.
Output :
1/((-t)^2+1)
Or input :
laplace(sin(t),t,s)
here the variable name is t and the variable name of the answer is s.
Output:
1/((-s)^2+1)
The following properties hold :
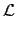 (y')(x) (y')(x) |
= |
- y(0) + x.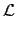 (y)(x) (y)(x) |
|
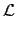 (y'')(x) (y'')(x) |
= |
- y'(0) + x.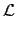 (y')(x) (y')(x) |
|
| |
= |
- y'(0) - x.y(0) + x2.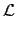 (y)(x) (y)(x) |
|
If
y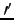 (x) + p.y
(x) + p.y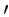 (x) + q.y(x) = f (x), then :
(x) + q.y(x) = f (x), then :
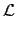 (f )(x) (f )(x) |
= |
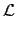 (y'' + p.y' + q.y)(x) (y'' + p.y' + q.y)(x) |
|
| |
= |
- y'(0) - x.y(0) + x2.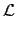 (y)(x) - p.y(0) + p.x. (y)(x) - p.y(0) + p.x.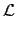 (y)(x)) + q. (y)(x)) + q.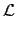 (y)(x) (y)(x) |
|
| |
= |
(x2 + p.x + q).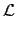 (y)(x) - y'(0) - (x + p).y(0) (y)(x) - y'(0) - (x + p).y(0) |
|
Therefore, if a = y(0) et b = y'(0), we have
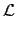
(
f )(
x) = (
x2 +
p.
x +
q).
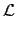
(
y)(
x) - (
x +
p).
a -
b
and the solution of the differential equation is :
y(
x) =
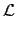 -1
-1((
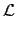
(
f )(
x) + (
x +
p).
a +
b)/(
x2 +
p.
x +
q))
Example :
Solve :
y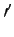
-6.
y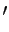
+9.
y =
x.
e3.x,
y(0) =
c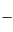
0,
y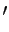
(0) =
c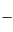
1
Here,
p = - 6, q = 9.
Input :
laplace(x*exp(3*x))
Output :
1/(x^ 2-6*x+9)
Input :
ilaplace((1/(x^2-6*x+9)+(x-6)*c_0+c_1)/(x^2-6*x+9))
Output :
(216*x^3-3888*x*c_0+1296*x*c_1+1296*c_0)*exp(3*x)/1296
After simplification and factorisation (factor command)
the solution y is :
(-18*c_0*x+6*c_0+x^3+6*x*c_1)*exp(3*x)/6
Note that this equation could be solved directly, input :
desolve(y''-6*y'+9*y=x*exp(3*x),y)
Output :
exp(3*x)*(-18*c_0*x+6*c_0+x^3+6*x*c_1)/6





suivant: Other functions
monter: Differential equations
précédent: Solving differential equations :
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse