Gauss-Jordan reduction: rref gaussjord

rref solves a linear system of equations written in matrix form (see also 1.31.17) :

A*X=B

rref takes one or two arguments.

• If rref has only one argument, this argument is the augmented matrix of the system (the matrix obtained by augmenting matrix A to the right with the column vector B).
  The result is a matrix [A1,B1] : A1 has zeros both above and under its principal diagonal and has 1 on its principal diagonal, and the solutions of:
  A1*X=B1
  are the same as :
  A*X=B
  For example, to solve the system:
  $$\left\{\vphantom{ \begin{array}{lcr} 3x + y & = &-2 \\ 3x +2y & =& 2 \end{array}}\right.$$$$\begin{array}{lcr} 3x + y & = &-2 \\ 3x +2y & =& 2 \end{array}$$
  input :
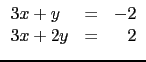
  rref([[3,1,-2],[3,2,2]])
  Output :
  [[1,0,-2],[0,1,4]]
  Hence x = - 2 and y = 4 is the solution of this system.

  rref can also solve several linear systems of equations having the same first member. We write the second members as a column matrix.
  Input :

  rref([[3,1,-2,1],[3,2,2,2]])
  Output :
  [[1,0,-2,0],[0,1,4,1]]
  Which means that (x = - 2 and y = 4) is the solution of the system
  $$\left\{\vphantom{ \begin{array}{lcr} 3x + y & = &-2 \\ 3x +2y & =& 2 \end{array}}\right.$$$$\begin{array}{lcr} 3x + y & = &-2 \\ 3x +2y & =& 2 \end{array}$$
  and (x = 0 and y = 1) is the solution of the system
  $$\left\{\vphantom{ \begin{array}{lcr} 3x + y & = &1 \\ 3x +2y & =& 2 \end{array}}\right.$$$$\begin{array}{lcr} 3x + y & = &1 \\ 3x +2y & =& 2 \end{array}$$

• If rref has two parameters, the second parameter must be an integer k, and the Gauss-Jordan reduction will be performed on (at most) the first k columns.
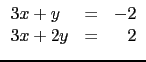
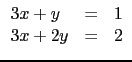
  Input :
  rref([[3,1,-2,1],[3,2,2,2]],1)
  Output :
  [[3,1,-2,1],[0,1,4,1]]