Find the matrix of an isometry : mkisom

mkisom takes as argument :

• In dimension 3, the list of characteristic elements (axis direction, angle for a rotation or normal to the plane for a symmetry) and +1 for a direct isometry or -1 an indirect isometry.
• In dimension 2, a characteristic element (an angle or a vector) and +1 for a direct isometry (rotation) or -1 for an indirect isometry (symmetry).

mkisom returns the matrix of the corresponding isometry.
Input :

mkisom([[-1,2,-1],pi],1)

Output the matrix of the rotation of axis [- 1, 2, - 1] and angle 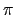$\pi$:

[[-2/3,-2/3,1/3],[-2/3,1/3,-2/3],[1/3,-2/3,-2/3]]

Input :

mkisom([pi],-1)

Output the matrix of the symmetry with respect to O :

[[-1,0,0],[0,-1,0],[0,0,-1]]

Input :

mkisom([1,1,1],-1)

Output the matrix of the symmetry with respect to the plane x + y + z = 0 :

[[1/3,-2/3,-2/3],[-2/3,1/3,-2/3],[-2/3,-2/3,1/3]]

Input :

mkisom([[1,1,1],pi/3],-1)

Output the matrix of the product of a rotation of axis [1, 1, 1] and angle 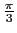${\frac{{\pi}}{{3}}}$ and of a symmetry with respect to the plane x + y + z = 0:

[[0,-1,0],[0,0,-1],[-1,0,0]]

Input :

mkisom(pi/2,1)

Output the matrix of the plane rotation of angle ${\frac{{\pi}}{{2}}}$ :

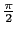[[0,-1],[1,0]]

Input :

mkisom([1,2],-1)

Output matrix of the plane symmetry with respect to the line of equation x + 2y = 0:

[[3/5,-4/5],[-4/5,-3/5]]