




suivant: Smith normal form :
monter: Matrix reduction
précédent: Hessenberg matrix reduction :
Table des matières
Index
Hermite normal form : ihermite
ihermite takes as argument a matrix A with coefficients
in 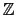 .
.
ihermite returns two matrices U and B such that
B=U*A, U is invertible in 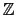 (det
(U) = ±1)
and B is upper-triangular. Moreover,
the absolute value of the coefficients above the diagonal of B are
smaller than the pivot of the column divided by 2.
(det
(U) = ±1)
and B is upper-triangular. Moreover,
the absolute value of the coefficients above the diagonal of B are
smaller than the pivot of the column divided by 2.
The answer is obtained by a Gauss-like reduction algorithm
using only operations of rows with integer coefficients
and invertible in 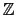 .
.
Input :
A:=[[9,-36,30],[-36,192,-180],[30,-180,180]]; U,B:=ihermite(A)
Output :
[[9,-36,30],[-36,192,-180],[30,-180,180]], [[13,9,7],[6,4,3],[20,15,12]],[[3,0,30],[0,12,0],[0,0,60]]
Application: Compute a 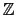 -basis of the kernel of a
matrix having integer coefficients
-basis of the kernel of a
matrix having integer coefficients
Let M be a matrix with integer coefficients.
Input :
(U,A):=ihermite(transpose(M)).
This returns U and A such that A=U*transpose(M) hence
transpose(A)=M*transpose(U).
The columns of transpose(A) which are identically 0 (at the right,
coming from the rows of A which are identically 0 at the bottom)
correspond to columns of transpose(U) which form a basis
of Ker(M). In other words, the rows of A
which are identically 0 correspond to rows of U
which form a basis of Ker(M).
Example
Let M:=[[1,4,7],[2,5,8],[3,6,9]]. Input
U,A:=ihermite(tran(M))
Output
U:=[[-3,1,0],[4,-1,0],[-1,2,-1]] and A:=[[1,-1,-3],[0,3,6],[0,0,0]]
Since A[2]=[0,0,0], a 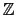 -basis of Ker(M) is
U[2]=[-1,2,-1].
-basis of Ker(M) is
U[2]=[-1,2,-1].
Verification M*U[2]=[0,0,0].





suivant: Smith normal form :
monter: Matrix reduction
précédent: Hessenberg matrix reduction :
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![]() .
.
![]() -basis of the kernel of a
matrix having integer coefficients
-basis of the kernel of a
matrix having integer coefficients