Make a sequence or a list : seq $

seq takes two, three, four or five arguments : the first argument is an expression depending of a parameter (for example j) and the remaining argument(s) describe which values of j will be used to generate the sequence. More precisely j is assumed to move from a to b:

• with a default step of 1 or -1: j=a..b or j,a..b (Maple-like syntax), j,a,b (TI-like syntax)
• or with a specific step: j=a..b,p (Maple-like syntax), j,a,b,p (TI-like syntax).

If the Maple-like syntax is used, seq returns a sequence, if the TI-like syntax is used, seq returns a list.

$ is the infixed version of seq when seq has only two arguments and returns always a sequence.
Remark:

• In Xcas mode, the precedence of $ is not the same as for example in Maple, in case of doubt put the arguments of $ in parenthesis. For example, the equivalent of seq(j^2,j=-1..3) is (j^2)$(j=-1..3) and returns (1,0,1,4,9). The equivalent of seq(4,3) is 4$3 and returns (4,4,4).
• With Maple syntax, j,a..b,p is not valid. To specify a step p for the variation of j from a to b, use j=a..b,p or use the TI syntax j,a,b,p and get the sequence from the list with op(...).

In summary, the different way to build a sequence are :

• with Maple-like syntax
  1. seq has two arguments either an expression depending of a parameter (for example j) and j = a..b where a and b are reals, or a constant expression and an integer n.
     seq returns the sequence where j is replaced in the expression by a, a + 1,...,b if b > a and by a, a - 1,...,b if b < a, or seq returns the sequence made by copying n times the constant.
  2. seq has three arguments an expression depending of a parameter (for example j) and j = a..b, p where a, b are reals and p is a real number.
     seq returns the sequence where j is replaced in the expression by a, a + p,...,b if b > a and by a, a - p,...,b if b < a.
     Note that j, a..b is also valid but j, a..b, p is not valid.
• TI syntax
  1. seq has four arguments an expression depending of a parameter (for example j), the name of the parameter (for example j), a and b where a and b are reals.
     seq returns the list where j is replaced in the expression by a, a + 1,...,b if b > a and by a, a - 1,...,b if b < a.
  2. seq has five arguments an expression depending of a parameter (for example j), the name of the parameter (for example j), a, b and p where a, b and p are reals.
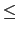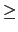     seq returns the list where j is substitued in the expression by a, a + p,...,a + k*p ( a + k*p $\leq$ b < a + (k + 1)*p or a + k*p $\geq$ b > a + (k + 1)*p). By default, p=1 if b > a and p=-1 if b < a.

Note that in Maple syntax, seq takes no more than 3 arguments and returns a sequence as in TI syntax, seq takes at least 4 arguments and returns a list.
Input to have a sequence with same elements :

seq(t,4)

Or :

seq(t,k=1..4)

Or :

t$4

Output :

(t,t,t,t)

Input to have a sequence :

seq(j^3,j=1..4)

Or :

(j^3)$(j=1..4)

Or :

seq(j^3,j,1..4)

Output :

(1,4,9,16)

Input to have a sequence :

seq(j^3,j=-1..4,2)

Output :

(1,1,9)

Or to have a list,
Input :

seq(j^3,j,1,4)

Output :

[1,4,9,16]

Input :

seq(j^3,j,0,5,2)

Output :

[0,8,64]

Input :

seq(j^3,j,5,0,-2)

or

seq(j^3,j,5,0,2)

Output :

[125,27,1]

Input :

seq(j^3,j,1,3,0.5)

Output :

[1,3.375,8,15.625,27]

Input :

seq(j^3,j,1,3,1/2)

Output :

[1,27/8,8,125/8,27]

Examples

• Find the third derivative of  ln(t), input:
  diff(log(t),t$3)
  Output :
  -((-(2*t))/t^4)
• Input :
  l:=[[2,3],[5,1],[7,2]]
  seq((l[k][0])$(l[k][1]),k=0 .. size(l)-1)
  Output :
  2,2,2,seq[5],7,7
  then eval(ans()) returns:
  2,2,2,5,7,7
• Input to transform a string into the list of its characters :

  f(chn):={
   local l;
   l:=size(chn);
   return seq(chn[j],j,0,l-1);
  }
  

  then input:
  f("abracadabra")
  Output :
  ["a","b","r","a","c","a","d","a","b","r","a"]