




suivant: Cyclotomic polynomial : cyclotomic
monter: Arithmetic and polynomials
précédent: Solving au+bv=c over polynomials:
Table des matières
Index
Chinese remainders : chinrem
chinrem takes two lists as argument, each list being made of 2
polynomials (either expressions or as a list of coefficients in decreassing
order). If the polynomials are expressions, an optionnal third
argument may be provided to specify the main variable, by default
x is used.
chinrem([A,R],[B,Q]) returns the list of two polynomials
P and S such that :
S = R.Q, P = A(mod R), P = B(mod Q)
If R and Q are coprime, a solution P always exists
and all the solutions are congruent modulo S=R*Q.
For example, assume we want to solve :
Input :
chinrem([[1,0],[1,0,1]],[[1,-1],[1,0,-1]])
Output :
[[1/-2,1,1/-2],[1,0,0,0,-1]]
or :
chinrem([x,x^2+1],[x-1,x^2-1])
Output :
[1/-2*x^2+x+1/-2,x^4-1]
hence
P(x) = - 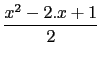 ( mod x4 - 1)
( mod x4 - 1)
Another example, input :
chinrem([[1,2],[1,0,1]],[[1,1],[1,1,1]])
Output :
[[-1,-1,0,1],[1,1,2,1,1]]
or :
chinrem([y+2,y^2+1],[y+1,y^2+y+1],y)
Output :
[-y^3-y^2+1,y^4+y^3+2*y^2+y+1]
giac documentation written by Renée De Graeve and Bernard Parisse
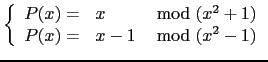
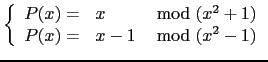
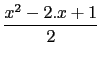 ( mod x4 - 1)
( mod x4 - 1)