




suivant: Euclidean remainder : rem
monter: Arithmetic and polynomials
précédent: Euclidean quotient : quo
Table des matières
Index
Euclidean quotient : Quo
Quo is the inert form of quo.
Quo returns the euclidean quotient between two polynomials
(decreasing power division) without evaluation.
It is used when Xcas is in Maple mode to compute
the euclidean quotient of the division of two
polynomials with coefficients in
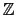 /p
/p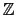 using Maple-like syntax.
using Maple-like syntax.
In Xcas mode, input :
Quo(x^2+2*x+1,x)
Output :
quo(x^2+2*x+1,x)
In Maple mode, input :
Quo(x^3+3*x,2*x^2+6*x+5) mod 5
Output :
-(2)*x+1)
The division was done using modular arithmetic, unlike with
quo(x^3+3*x,2*x^2+6*x+5) mod 5
where the division is done in
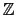 [X] and reduced after to:
[X] and reduced after to:
3*x-9
If Xcas is not in Maple mode, polynomial division
in
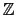 /p
/p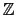 [X] is done e.g. by :
[X] is done e.g. by :
quo((x^3+3*x)% 5,(2x^2+6x+5)%5)
giac documentation written by Renée De Graeve and Bernard Parisse