Polynomials

A polynomial of one variable is represented either by a symbolic expression or by the list of it's coefficients by decreasing powers order (dense representation). In the latter case, to avoid confusion with other kinds of list

• use poly1[...] as delimiters in inputs
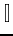
• check for 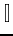$\talloblong$ $\talloblong$ in Xcas output.

Note that polynomials represented as lists of coefficients are always written in decreassing powers order even if increasing power is checked in cas configuration.

A polynomial of several variables is represented

• by a symbolic expression
• or by a dense recursive 1-d representation like above
• or by a sum of monomials with non-zero coefficients (distributed sparse representation).
  A monomial with several variables is represented by a coefficent and a list of integer (interpreted as powers of a variable list). The delimiters for monomials are %%%{ and %%%}, for example 3x²y is represented by %%%{3,[2,1]%%%} with respect to the variable list [x,y]).