




suivant: The properties of the
monter: Fourier transformation
précédent: fourier_cn
Table des matières
Index
Let N be an integer.
The Discrete Fourier Transform (DFT) is a transformation FN defined on
the set of periodic sequences of period N, it depends on a choice
of a primitive N-th root of unity 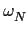 . If the
DFT is defined on sequences with complex coefficients, we take:
. If the
DFT is defined on sequences with complex coefficients, we take:
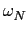
=
e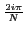
If x is a periodic sequence of period
N, defined by the vector
x = [x0, x1,...xN-1] then
FN(x) = y is a periodic sequence of period N, defined by:
(
FN,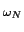
(
x))
k =
yk =
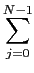 xj
xj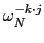
,
k = 0..
N - 1
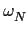 is a primitive N-th root of unity.
The discrete Fourier transform may be computed faster than by
computing each yk individually, by the Fast Fourier Transform (FFT).
Xcas implements the FFT algorithm to compute
the discrete Fourier transform only if N is a power of 2.
is a primitive N-th root of unity.
The discrete Fourier transform may be computed faster than by
computing each yk individually, by the Fast Fourier Transform (FFT).
Xcas implements the FFT algorithm to compute
the discrete Fourier transform only if N is a power of 2.
Sous-sections
giac documentation written by Renée De Graeve and Bernard Parisse