




suivant: fourier_an
monter: Fourier transformation
précédent: Fourier transformation
Table des matières
Index
Fourier coefficients : fourier_an and fourier_bn or fourier_cn
Let f be a T-periodic continuous functions on
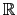 except maybe at a finite number of points.
One can prove that if f is continuous at x, then;
except maybe at a finite number of points.
One can prove that if f is continuous at x, then;
| f (x) |
= |
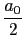 + + 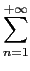 ancos( ancos(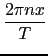 ) + bnsin( ) + bnsin(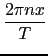 ) ) |
|
| |
= |
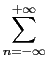 cne cne 2i 2i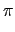 nxT nxT |
|
where the coefficients an, bn, n 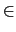 N, (or cn, n
N, (or cn, n 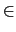 Z) are the
Fourier coefficients of f.
The commandsfourier_an and fourier_bn or fourier_cn
compute these coefficients.
Z) are the
Fourier coefficients of f.
The commandsfourier_an and fourier_bn or fourier_cn
compute these coefficients.
Sous-sections
giac documentation written by Renée De Graeve and Bernard Parisse