




suivant: Change of variables :
monter: Integration by parts :
précédent: ibpdv
Table des matières
Index
ibpu
ibpu is used to search the primitive of an expression written
as
u(x).v'(x)
ibpu takes two arguments :
- an expression
u(x).v'(x) and u(x) (or a list of two expressions
[F(x), u(x)*v'(x)] and u(x)),
- an expression g(x) and 0 (or a list of two expressions
[F(x)g(x)]
and 0).
ibpu returns :
- if
u(x)
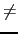 0, the list
[u(x).v(x), - v(x).u'(x)]
(or returns the list
[F(x) + u(x).v(x), - v(x).u'(x)]),
0, the list
[u(x).v(x), - v(x).u'(x)]
(or returns the list
[F(x) + u(x).v(x), - v(x).u'(x)]),
- if the second argument is zero, a primitive of the first argument g(x)
(or F(x)+a primitive of g(x)):
ibpu(g(x),0) returns G(x) where diff(G(x))=g(x) or
ibpu([F(x),g(x)],0) returns F(x)+G(x) where diff(G(x))=g(x).
Hence, ibpu returns the terms computed in an integration by parts,
with the possibility of doing several ibpu succesively.
When the answer of ibpu(u(x)*v'(x),u(x)) is computed, to obtain a
primitive of
u(x).v'(x), it remains to
compute the integral of the second term of this answer and then, to sum this
integral with the first term of this answer : to do this, just use
ibpu command with the answer as first argument and
a new u(x) (or 0 to terminate the integration) as second argument.
Input :
ibpu(ln(x),ln(x))
Output :
[x.ln(x),-1]
then
ibpu([x.ln(x),-1],0)
Output :
-x+x.ln(x)
Remark
When the first argument of ibpu is a list of two elements, ibpu
works only on the last element of this list and adds the integrated term to
the first element of this list.
(therefore it is possible to do several ibpu successively).
For example :
ibpu((log(x))^2,log(x)) = [x*(log(x))^2,-(2*log(x))]
it remains to integrate -(2*log(x)), hence input :
ibpu(ans(),log(x))
or input :
ibpu([x*(log(x))^2,-(2*log(x))],log(x))
Output :
[x*(log(x))^2+x*(-(2*log(x))),2]
it remains to integrate 2, hence input :
ibpu(ans(),0) or input :
ibpu([x*(log(x))^2+x*(-(2*log(x))),2],0).
Output :
x*(log(x))^2+x*(-(2*log(x)))+2*x





suivant: Change of variables :
monter: Integration by parts :
précédent: ibpdv
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse