Scatterplots

20.2.2 Scatterplots

A scatter plot is simply a set of points plotted on axes. The scatterplot or nuage_points command draws scatter plots.

scatterplot takes two arguments: xcoords and ycoords, a list of x-coordinates and y-coordinates. You can also combine them into a matrix with two columns (each list becomes a column of the matrix).
scatterplot(xcoords,ycoords) draws the points with the given coordinates.

The batons command will also draw a collection of points, but each point will be connected to the x-axis with a vertical line segment.

batons takes two arguments: xcoords and ycoords, a list of x-coordinates and y-coordinates. You can also combine them into a matrix with two columns (each list becomes a column of the matrix).
batons(xcoords,ycoords) draws the points with the given coordinates and connects them to the x-axis with vertical line segments.

Examples

scatterplot([[0,0],[1,1],[2,4],[3,9],[4,16]],display=point_width_3+point_point+red)

or:

scatterplot([0,1,2,3,4],[0,1,4,9,16],display=point_width_3+point_point+red)

batons([[0,0],[1,1],[2,4],[3,9],[4,16]])

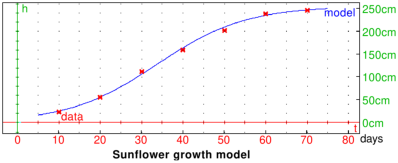
As a practical example, assume that a model of the growth of a sunflower is given by the formula:

h(t)=

256

1+23e^−0.093t

where t is time in days and h is plant height in centimeters. The measured height is given in the following table:

t (days)	10	20	30	40	50	60	70
h (cm)	23	56	112	160	203	239	246

To define the function h, enter:

h(t):=256/(1+23*exp(-0.093*t)):;

To load the data, enter:

tdata:=[10,20,30,40,50,60,70]:; hdata:=[23,56,112,160,203,239,246]:;

To display the model together with data, enter:

title="*Sunflower growth model*"; labels=["t","h"]; legend=["days","cm"]; plotfunc(h(t),t=5..75,color=blue+quadrant4,legend="model"); scatterplot(tdata,hdata,display=star_point+point_width_2+red+quadrant4,legend="data");