Contour lines

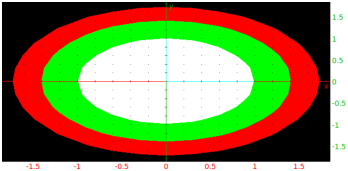
The plotcontour or DrwCtour or contourplot command draws contour lines for functions of two variables.

plotcontour takes two mandatory arguments and one optional argument:
- expr, an expression involving two variables.
- vars, a list of the two variables.
- Optionally, values, a list of values of the contour lines to draw; expr=value, for value in values (by default, [−10,−8,…,8,10]).
plotcontour(expr,vars ⟨,values ⟩) draws the contour lines expr=value for value in values.

plotcontour(x^2+y^2,[x=-3..3,y=-3..3],[1,2,3],display=[green,red,black]+[filled$3])

plotcontour(x^2-y^2,[x,y])

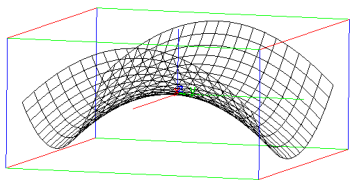
If you want to draw the surface in 3D representation, use plotfunc (see Section 19.2.2).

plotfunc(x^2-y^2,[x,y])