8.14.2  3D parametric surface: plotparam paramplot DrawParm

To draw a parametric surface in ℝ³:

• plotparam takes two mandatory arguments and two optional arguments:
  • exprs, a list of three expressions involving two parameters.
  • vars, a list of the parameters, optionally with a range var=a..b.
  • Optionally, ustep=n, to set the discretization step of the first parameter.
  • Optionally, vstep=m, to set the discretization step of the second parameter.
• plotparam(exprs,vars ⟨ ,ustep=n,vstep=m⟩) draws the parametric representation of the surface.

Examples.

• Input:
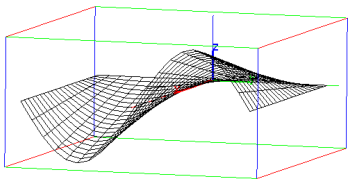
  plotparam([v*cos(u),v*sin(u),v],[u,v])
  Output:
  
• Input:
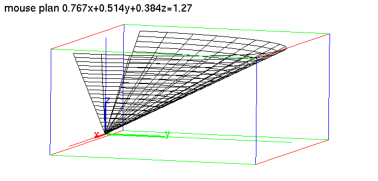
  plotparam([v*cos(u),v*sin(u),v],[u=0..pi,v=0..3])
  Output:
  
• Input:
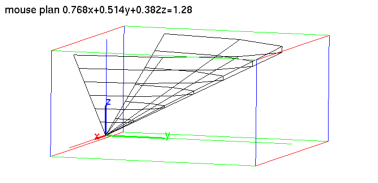
  plotparam([v*cos(u),v*sin(u),v],[u=0..pi,v=0..3],ustep=0.5,vstep=0.5)
  Output: