Capes 2011 et XcasRenee.Degraeve@wanadoo.fr2010 |
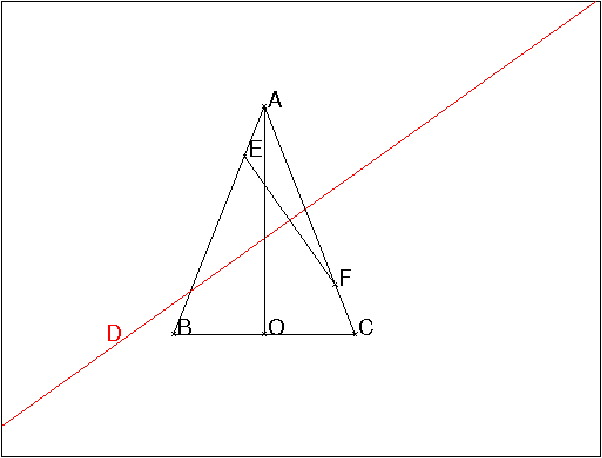
Soit ABC un triangle isocèle en A et soit E un point de [AB]. On considère le point F de [AC] tel que AF = BE. On note (D) la médiatrice de [EF ]. On se propose de montrer que, lorsque E décrit [AB], la médiatrice de [EF ] passe par un point fixe.
Lorsque E est en B, F est en A et donc la médiatrice de [EF ] est la médiatrice de [AB].
Lorsque E est en A, F est en C et donc la médiatrice de [EF ] est la médiatrice de [AC].
Le point fixe est donc le point d’intersection des médiatrices de [AB] et [AC] c’est à dire le centre du cercle circonscrit au triangle ABC.
Pour faire la figure, on ouvre un niveau de géométrie (Alt+g) et on tape (O est le milieu de BC) :
A:=point(5*i); B:=point(-2); C:=point(2); triangle(A,B,C); O:=milieu(B,C); t:=element(0..1); E:=element(segment(B,A),t); F:=inter_unique(segment(A,C),cercle(C,longueur(A,E))); segment(E,F); D:=mediatrice(E,F,affichage=1); segment(A,O);
On obtient :

et si on rajoute la commande :
trace(D)
On obtient :
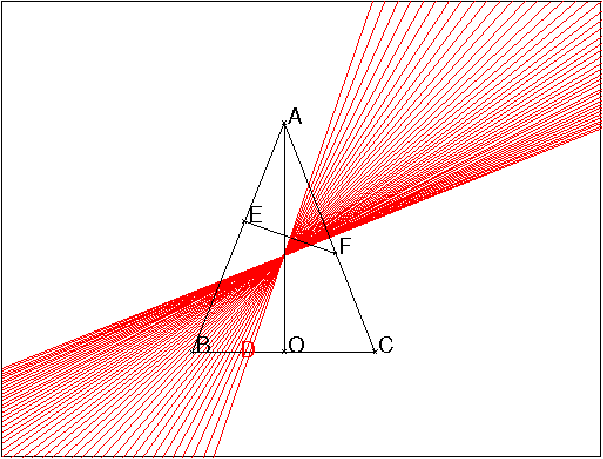
Puis on fait bouger t à l’aide du curseur et on voit que la
médiatrice de EF, semble passer par un point fixe I situé sur
la bissectrice de l’angle BAC.
Il y a différentes façons de continuer.
Par exemple, au départ sans utiliser de transformation) :
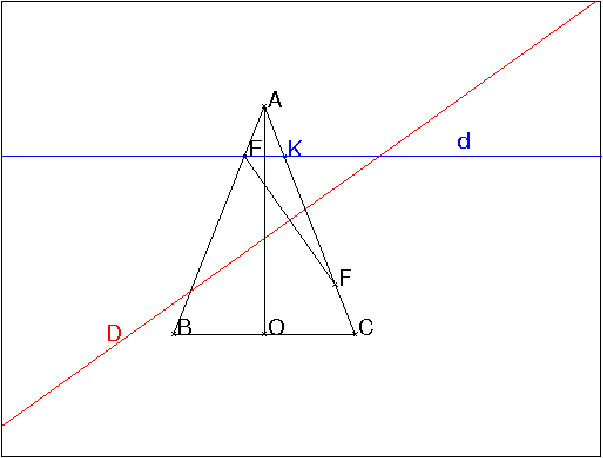
Les médiatrices du triangle EFK sont
D (la médiatrice de EF), AO (la médiatrice de EK) et la médiatrice
de KF. Le triangle AEK est isocèle donc AK=FC donc la médiatrice
de KF est aussi la bissectrice de l’angle BAC.
AK=CF donc la médiatrice de KF est aussi la médiatrice de AC.
Les médiatrices du triangle EFK se coupent en un même point
donc la médiatrice de EK passe par le point d’intersection de la
bissectrice de l’angle BAC et de la médiatrice de AC.
On voit avec cette démonstration que l’hypothèse "le triangle ABC est
isocèle" ne sert pas.
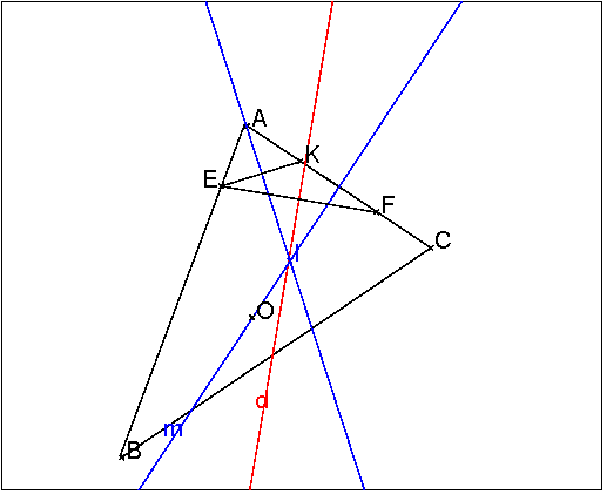
E1:=symetrie(droite(A,O),E);segment(A,O); F1:=symetrie(droite(A,O),F); segment(E1,F1); D1:=mediatrice(E1,F1,affichage=1); I:=inter_unique(D,D1,affichage=1);On obtient :

Puis on fait bouger t à l’aide du curseur et on voit que le point
I intersection des médiatrices de EF et de E1F1 est fixe.
Comment définir ce point ?
I est le centre du cercle circonscrit à EF1E1F donc c’est aussi
l’interscetion des médiatrices de EF1 et de E1F.
Puisque AE=BF1 la médiatrice de EF1 est aussi la médiatrice de
AB.
Puisque AE1=CF la médiatrice de E1F est aussi la médiatrice de
AC
donc I intersection des médiatrices de AB et de AC est fixe
et c’est le centre du cercle circonscrit au triangle ABC.
On tape alors :
J:=centre(circonscrit(A,B,C));
pour voir que I et J sont confondus.
Dans la réponse proposée par l’élève :
Le point fixe est donc le point d’intersection des médiatrices de [AB] et [AC] c’est à dire le centre du cercle circonscrit au triangle ABC.
il faut contester le donc en le remplaçant la réponse par :
si la médiatrice de EF passe par un point fixe, ce point fixe doit être le point d’intersection des médiatrices de [AB] et [AC] c’est à dire le centre du cercle circonscrit au triangle ABC. Il reste à le démontrer
Pour convaincre l’éléve on peut refaire le même exercice avec
F sur AC mais avec CF=AE/2. On cherche les positions limites et cela ne
donne rien car la médiatrice de EF ne passe pas par un point fixe....
On fait la figure correspondante en mettant pour définir F :
F:=inter_unique(segment(A,C),cercle(C,longueur(A,E)/2));
et on observe la trace de D, on obtient :
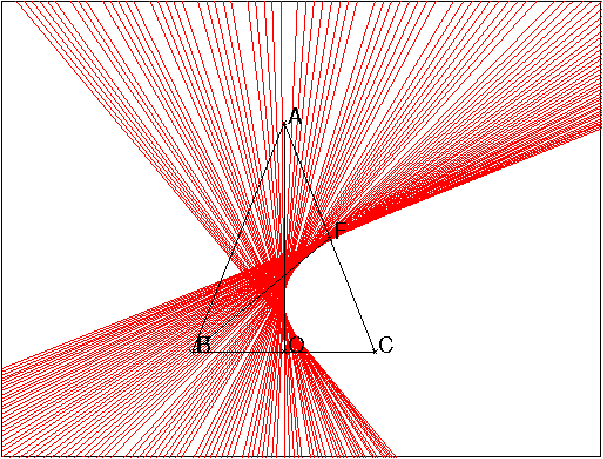
une belle enveloppe !!!
En tant qu’outils de démonstration, les exercices faisant appel aux
transformations sont difficiles car une transformation n’est souvent pas
visible....
Par contre quand on a trouvé la transformation, tout devient limpide et
facile...
Voici quelques exercices classiques (On se reportera au manuel de géométrie
de Xcas pour les démonstrations) :
Problèmes de construction
Le théorème GH=2OG
Soit un triangle A,B,C et soientt A1,B1,C1 les milieux respectifs de BC,
AC, AB.
Soient G son centre de gravité, H son orthocentre et O le centre de
son cercle circonscrit.
L’homothétie h de centre G et de rapport -2 transforme A1 en A, (resp
B1 en B) et donc puisque l’homothétie conserve les angles, h transforme
la médiatrice de BC en la hauteur issue
de A (resp donc transforme la médiatrice de AC en la hauteur issue
de B) donc transforme le centre le centre O de
son cercle circonscrit en l’orthocentre H donc :
GH=−2GO
Le théorème de 1968
Soit un triangle quelconque direct ABC.
On construit sur les côtés du triangle ABC les carrés directs
CBDE, ACFG et BAKH, puis les parallélogrammes FCDJ et EBKL.
Alors le triangle AJL est isocèle rectangle direct.
Le théorème de Napoléon
Soit un triangle quelconque ABC.
On construit à l’extérieur du triangle ABC les triangles équilatèraux
BAD, CBE et ACF qui ont pour centre de gravité : G1, G2 et G3.
On a les propriétés suivantes :
Le triangle G1G2G3 est équilatéral et a même centre de gravité que
le triangle ABC.
Les droites AE, DC, BF sont concourantes en un point T qui s’appelle le
point de Torricelli.
Le point T est aussi le point de concours des cercles circonscrits aux
triangles BAD, CBE et ACF.
On trouve dans le manuel Déclic - Terminale S, enseignement obligatoire (Hachette 2006), dans le chapitre « Fonctions - Variations et continuité », l’énigme suivante :
Un marcheur a parcouru 10 km en une heure. Existe-t-il un intervalle d’une demi-heure pendant lequel il a parcouru exactement 5 km ?
Pour guider les élèves dans la résolution de l’énigme, le manuel
Déclic propose l’exercice ci-dessous.
Pour t appartenant à l’intervalle [0;1], on désigne par f(t) la
distance, en kilomètres, parcourue à l’instant t, en heures.
Il est naturel de faire l’hypothèse que f est une fonction continue sur
[0;1].
| g(t)=f(t+ |
| )−f(t) |
On a : f(0)=0 et f(1)=10 et f est continue et croissante.
On cherche a pour que :
g(a)=f(a+1/2)−f(a)=5 avec g(t)=f(t+1/2)−f(t).
On a :
g(0)=f(1/2) et g(1/2)=10−f(1/2)
Si g(0)=f(1/2)>5 alors g(1/2)=(10−f(1/2))≤ 5 et alors
5∈ [g(1/2);g(0)] et comme g est continue d’après le théorème
des valeurs intermédiaires, il existe a dans l’intervalle
[0;1/2] tel que g(a)=5.
Si g(0)=f(1/2)<5 alors g(1/2)=(10−f(1/2))≥ 5 et alors
5∈ [g(0);g(1/2)] et comme g est continue d’après le théorème des
valeurs intermédiaires, il existe a dans l’intervalle [0;1/2]
tel que g(a)=5.
Pour que l’exercice soit moins théorique on va faire cet exercice sur
3 exemples en prenant succéssivement :
^2f1(x):=10*x^2; plotfunc(f1(x),x=0..1); g1(x):=f1(x+0.5)-f1(x); plotfunc(g1(x),x=0..1/2); droite(y=5,affichage=4); a1:=solve(g1(x)=5,x)[0]; droite(x=a1,affichage=1); droite(x=a1+0.5,affichage=1); f1(a1+0.5)-f1(a1);On obtient :
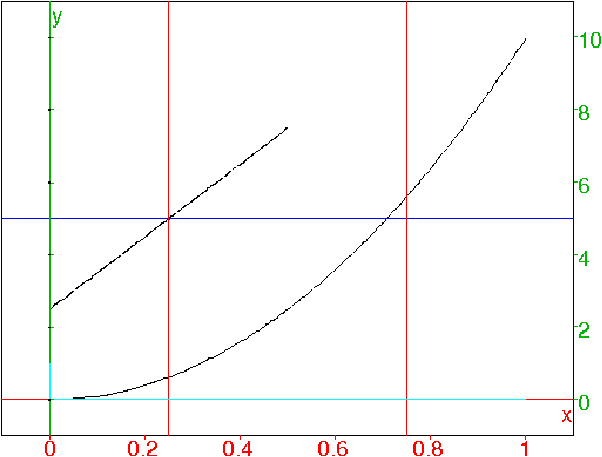
^3f2(x):=10*x^3; plotfunc(f2(x),x=0..1); g2(x):=f2(x+0.5)-f2(x); plotfunc(g2(x),x=0..1/2); droite(y=5,affichage=4); a2:=solve(g2(x)=5,x)[1] droite(x=a2,affichage=1); droite(x=a2+0.5,affichage=1); f2(a2+0.5)-f2(a2);On obtient :
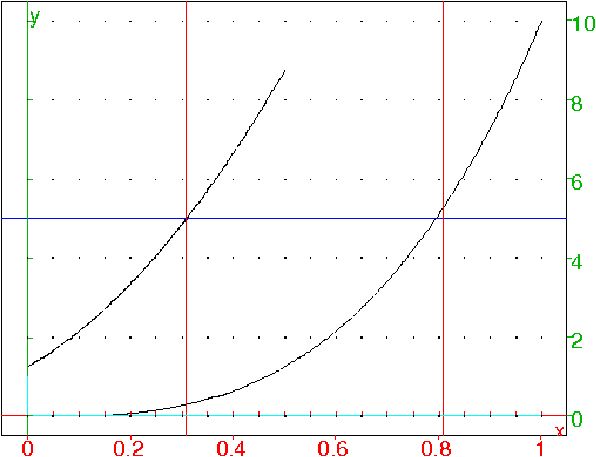
^2,2*x+8)f3(x):=ifte(x<0.5,36*x^2,8+2*x); plotfunc(f3(x),x=0..1); g3(x):=-36*x^2+2*x+9.)); plotfunc(g3(x),x=0..1/2); droite(y=5,affichage=4); a3:=solve(g3(x)=5,x)[1]; droite(x=a3,affichage=1); droite(x=a3+0.5,affichage=1); f3(a3+0.5)-f3(a3);On obtient :

Le plan est rapporté à un repère orthonormal direct
(A; AB, AD).
On considère le carré ABCD et les points E et F tels que ABE et
CBF soient des triangles équilatéraux directs.
Mathématiques - Terminale scientifique arrêté du 20-7-2001.
BO no 4 du 30 août 2001(...)
II. 2 Géométrie
L’objectif de ce paragraphe est d’entretenir la pratique des
objets usuels du plan et de l’espace et de fournir quelques notions nouvelles
permettant de parfaire l’approche entreprise dans les classe antérieures sur
la géométrie vectorielle ou repérée. Dans le prolongement du repérage
polaire introduit en première, les nombres complexes, outre leur intérêt
historique, algébrique et interdisciplinaire pour la poursuite des études,
fournissent un outil efficace dans les problèmes faisant intervenir les
transformations planes. L’extension à l’espace du produit scalaire permet de
résoudre de nouveaux problèmes et, de ce fait, d’approfondir la vision de
l’espace.
Bien que, comme dans les programmes antérieurs, le libellé de cette partie
soit relativement concis, on prendra le temps de mettre en oeuvre toutes les
connaissances de géométrie de l’ensemble du cursus scolaire pour l’étude
de configurations du plan ou de l’espace, le calcul de distances, d’angles,
d’aires et de volumes, etc. Ces travaux seront répartis tout au long de
l’année afin que les élèves acquièrent une certaine familiarité avec
le domaine géométrique ; on privilégiera les problèmes dont les
procédés de résolution peuvent avoir valeur de méthode et on entraînera
les élèves à choisir l’outil de résolution le plus pertinent parmi ceux
dont ils disposent (propriétés des configurations, calcul vectoriel, calcul
barycentrique, transformations, nombres complexes, géométrie analytique).
Le triangle ABE est équilatéral de côté 1, donc
E a comme affixe : exp(i*π/6)=1/2+i√3/2
On a : AE=AB+BE.
AB a comme affixe 1 et BE a comme affixe
exp(i*π/3)=i/2+√3/2 donc
F a comme affixe : 1+√3/2+i/2
donc EF2=(1/2+√3/2)2+(−1/2+√3/2)2=2 (
ce qui etait évident puisque EF est l’hypoténuse d’un triangle rectangle
isocèle de côté 1).
DE a donc comme affixe 1/2+i(√3/2−1)
DF a donc comme affixe :1+√3/2−i/2)
On a :
1+√3/2−i/2)=(2+√3)(1/2−i/2/(2+√3)=(2+√3)(1/2−i/2(2−√3)
donc DF=(2+√3)DE)
c’est à dire que D,E,F sont alignés.
On a donc :
DF=(2+√3)DE et
EF=−DE+(2+√3)DE=(1+√3)DE
EF=√2 donc
DE=√2(√(3−1))/2 et
DF=(√3+2)DE=√2(1+√3)/2
donc
DF=DE+EF
La rotation de centre B et d’angle π/3 transforme :
E en A, F en C et D en D1.
Le triangle D1DB est donc équilatéral donc D1 est sur la médiatrice
de DB. Puisque ABCD est un carré ses diagonales se coupent en leur
milieu I et sont perpendiculaires, AC est la médiatrice de DB.
Donc D1,A,C sont alignés.

On se sert des propiétés des rotations :
La rotation de centre B et d’angle −π/3 transforme le point x;y en :
[[1/2,sqrt(3)/2],[−sqrt(3)/2,1/2]] *[x−1,y]+[1,0].
E est le transformé de A=(0;0) par la rotation de centre B et d’angle
−π/3 donc E a pour coordonnées :
[[1/2,sqrt(3)/2],[-sqrt(3)/2,1/2]] *[-1,0]+[1,0]
c’est à dire [1/2,(sqrt(3))/2]
F est le transformé de C=(1;1) par la rotation de centre B et d’angle
−π/3 donc F a pour coordonnées :
[[1/2,sqrt(3)/2],[-sqrt(3)/2,1/2]] *[0,1]+[1,0]
c’est à dire [(sqrt(3))/2+1,1/2]
D1,A,C sont alignés donc D,E,F sont alignés.
D1,A,C sont sont alignés dans cet ordre donc D,E,F sont alignés dans
cet ordre.
D1I=√2*√3/2 comme hauteur d’un triangle équilatéral de côté
√2.
IA=IC=√2/2 comme demi-diagonale d’un carré de côté 1.
DF=D1C=D1I+IC=√6/2+√2/2
DE=D1A=D1I−IA=√6/2−√2/2
EF=AC=√2
Dans le triangle BEF, l’angle B vaut π/2 et BF=BE=1 donc
EF2=BF2+BE2=2.
Donc EF=√2
Dans le triangle ADE, l’angle A vaut π/6 et AD=AE=1 donc :
DE2=AD2+AE2−2AD*AE*cos(π/6)=2−√3.
Donc DE=(√6−√2)/2
Dans le triangle CDF, l’angle A vaut π/2+π/3 et CD=CF=1 donc :
DF2=CD2+CF2+2CD*CF*sin(π/3)=2+√3.
Donc DF=(√6+√2)/2
On tape dans un écran de géométrie :
A:=point(0); B:=point(1); carre(A,B,C,D); triangle_equilateral(A,B,E); triangle_equilateral(C,B,F);
On obtient :
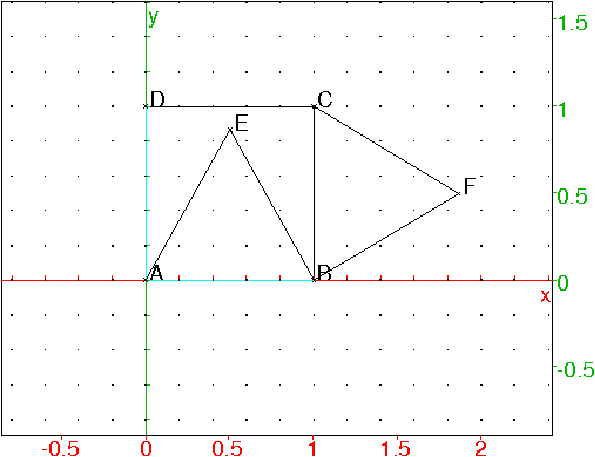
On tape :
coordonnees(E);
On obtient :
[1/2,(sqrt(3))/2]
On tape pour avoir l’affixe de E:
normal(affixe(E));
On obtient :
((i)*sqrt(3)+1)/2
On tape :
coordonnees(F);
On obtient :
[1+(sqrt(3))/2,1/2]
On tape pour avoir l’affixe de F:
normal(affixe(F));
On obtient :
sqrt(3)+2+i)/2
On tape :
est_aligne(D,E,F);
On obtient :
1
On tape :
normal(longueur2(D,E));
On obtient :
-sqrt(3)+2
On a puisque 22−3=1 est un carré parfait :
√(2−√3)=√2/2(√(2+1)−√(2−1)) et
√(2+√3)=√2/2(√(2+1)+√(2−1))
donc DE=√2−√3=√2(√3−1)/2
On tape pour avoir l’affixe de DE:
normal(E-D);
On obtient :
((i)*sqrt(3)+1-2*i)/2
On tape pour avoir la norme au carré de DE:
normal(abs(E-D)^2);
On obtient :
-sqrt(3)+2
On tape :
normal(longueur2(E,F));
On obtient :
2 donc EF=√2
On tape pour avoir la norme de EF:
normal(abs(F-E));
On obtient :
sqrt(2)
On tape :
normal(longueur2(D,F));
On obtient :
sqrt(3)+2
donc DF=√2+√3=√2(√3+1)/2
donc DF=DE+EF
On tape pour avoir l’affixe de DF:
normal(F-D);
On obtient :
(sqrt(3)+2-i)/2
On tape pour avoir la norme au carré de DF:
normal(abs(F-D)^2);
On obtient :
sqrt(3)+2
Remarque
L’égalité algébrique peut se déduire du fait que D,E,F sont alignés.
En effet :
E se trouve à l’intérieur du carré ABCD donc dans le même
demi-plan limité par BC que D alors que
F se trouve dans l’autre demi-plan,
donc D,E,F sont dans cet ordre sur la droite DE
27.42−212=309.76
C’est l’aire OB2
√309.76=17.6
17.6*2=35.2
L’autre diagonale mesure :35.2
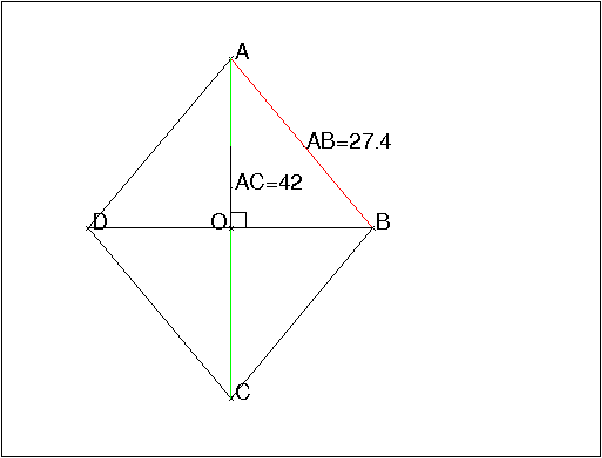
Croquis :
Il faut que l’élève cite les théorèmes :
L’élève doit préciser que l’unité choisie est ici le cm et dire :
l’aire OB2 est de 27.42−212=309.76 cm
donc OB mesure √309.76=17.6 cm et donc l’autre diagonale mesure
35.2 cm. On remarque que 17.62=309.76 donc le calcul est exact.
On tape dans un niveau de géométrie :
A:=point(0,21); B:=point(17.6); C:=point(0,-21); D:=point(-17.6); polygone(A,B,C,D); O:=point(0); E:=point(17.6/3,14); F:=point(-17.6/3,-14); d:=droite(E,F):;d; d1:=demi_droite(D,A):;d1; d2:=demi_droite(B,C):;d2; I:=inter_unique(d,d1); J:=inter_unique(d,d2);
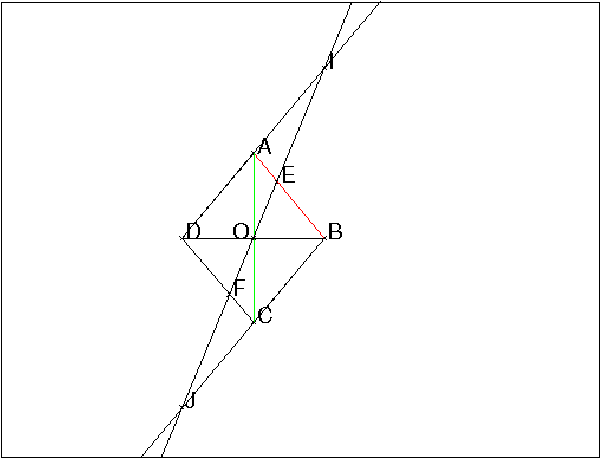

Dans cette démonstration on ne se sert pas du point F et on considère
h l’homothétie de centre D et de rapport 2.

On définit K par K=h(A).
h transforme O en B et A en K, donc transforme la droite OA en la
droite BK paralléle à OA. OA est perpendiculaire à OB donc
BK est perpendiculaire à OB donc BDK est un triangle rectangle
Pour montrer que BDI est un triangle rectangle, on va montrer que K et I
sont confondus :
Le point E est le centre de gravité du triangle DBK car il est situé
sur la médiane AB de ce triangle DBK et que AE=AB/3. Donc la médiane
KO de ce triangle DBK passe pae E et ainsi K,E,O sont alignés et K
et I sont alignés.
Le plan est rapporté à un repère orthonormal direct
(O; i, j).
Pour tout réel t, on note M (t) le point de coordonnées :
| ⎧ ⎨ ⎩ |
|
et on note V(t) le vecteur de coordonnées (x′(t), y′(t).
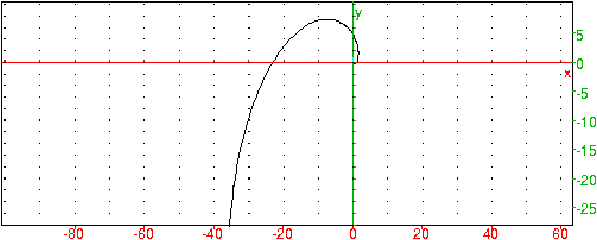
O:=point(0); supposons(t=[2.7,-5,5,0.1]); M:=point(r(t)); T:=point(s(t)+r(t)); vecteur(M,T); plotparam(r(t),t=-5..5); segment(O,M); N:=point(s(t)-r(t)); vecteur(M,N); K:=homothetie(M,-1,O); vecteur(M,K);On obtient:

^50
ou
(2 mod 10)^50^10, 2^10 mod 10)^5=2^10Ou encore
On peut aussi deviner que k=26 est une solution puisque 2*26-1=51
On cherche des entiers k et p vérifiant : 2k−1=51p et
comme 2*26−1=51, cela revient à chercher :
des entiers k et p vérifiant : 2(k−26)=51(p−1) et puisque 2 et 51
sont premiers entre eux, k−26est un multiple de 51 donc
k−26=51*m avec m≥ 0
Les propositions suivantes sont indépendantes. Préciser pour chacune d’elles si elle est vraie ou fausse. Justifier.
Mathématiques - Série scientifique
BO no 7 du 31 août 2000(...)
Le monde mathématique de chaque élève s’élabore en grande
partie à travers une pratique permanente de calculs, d’argumentations, de
petits raisonnements et de démonstrations. Le niveau de rigueur exigible pour
une démonstration dépend de l’expérience de l’élève dans le domaine où
cette démonstration se situe : ainsi, pour la géométrie, pratiquée
depuis l’école primaire, on peut prétendre exiger dès la classe de
seconde un niveau de démonstration académique ; en analyse, par contre, la
plupart des objets manipulés ne sont pas définis formellement à ce niveau
d’études, et les élèves ne peuvent pas aboutir à des démonstrations
parfaitement achevées : la nature et le niveau des rédactions exigibles ne
peuvent pas être les mêmes. Il conviendra donc, à ce niveau d’étude, en
particulier en analyse, d’accepter des argumentations conçues et exposées à
l’aide de schémas (même si les élèves ne peuvent pas à ce stade les
traduire en un texte linéaire). On gardera néanmoins l’état d’esprit
déjà évoqué dans les programmes de collège et de seconde : repérer
clairement le statut des divers énoncés en jeu (définition, axiome,
théorème démontré, théorème admis,...).
La déduction usuelle (par implication ou équivalence) et la manipulation du
contre-exemple ont été travaillées en seconde ; des problèmes bien
choisis permettront d’aborder en première le raisonnement par contraposition,
par l’absurde ou par disjonction des cas ; le raisonnement par récurrence
relève de la classe de terminale.
La démonstration doit garder un caractère vivant et personnel et il
convient d’éviter qu’elle n’apparaisse comme une activité relevant d’un
protocole trop rigide. Chaque année, les assertions qui doivent être
justifiées dans le cadre d’une pratique de la démonstration changent : il
est difficile pour les élèves de cerner, parmi les éléments qui
devaient être justifiés les années précédentes, ceux
qui deviennent des évidences, pour lesquelles une justification ne ferait
qu’alourdir la démonstration
^2,k=1..n))^2+n)Ce document a été traduit de LATEX par HEVEA