



Next: First order equations.
Up: Linear differential equations (systems)
Previous: Inverse laplace transform.
Linear differential equations systems with constant
coefficients.
Example: suppose we want to solve the following system:
with initial data
y1(0)=y2(0)=0.
For scalar linear differential equations with constant coefficients,
it is a well-known procedure to use Laplace transform, e.g. to solve
a y'' + b y' + c y = f(x)
one would perform the 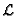 -transform and get:
-transform and get:
where f(0) and f'(0) are the initial consitions at x=0.
If
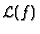 is a rational fraction,
is a rational fraction, ILAP allows you to recover
y by inverse Laplace transform of
But this method may be applied to systems of linear differential
equations as well.
The aim of LDEC is to help you solving 1st order systems
(note that higher order systems may always be rewritten as 1st order
systems).
Let
y=(y1, ..., yn) be a vector of functions of x and suppose
that we want to solve:
y' = A y + b
where A is a
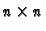 constant matrix and
b a vector of n functions of x.
Denote by
constant matrix and
b a vector of n functions of x.
Denote by
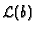 the vector of the n Laplace transform of the
n functions of b , and by y(0) the vector of n initial data at
x=0 .
Then
the vector of the n Laplace transform of the
n functions of b , and by y(0) the vector of n initial data at
x=0 .
Then
(I denotes the identity matrix), hence:
and:
![\begin{displaymath}
y={\cal L}^{-1} \left[ ( s I - A )^{-1} ( {\cal L}(b) ) \right]
+ {\cal L}^{-1}\left[ (sI-A)^{-1} y(0) \right]
\end{displaymath}](img116.gif) |
(1) |
The purpose of LDEC is to compute
the solution with initial data y(0)=0,
given A and b.
The stack should be prepared as:
stk2: b
stk1: A,
then type LDEC and you will get y at stack level 1.
Stack level 3 is the comatrix, stack level 2 is the determinant of (sI-A).
Let's do it for the example above:
First put b on the stack: { 1 'EXP(X)' }
(here VX is set as usual to 'X').
Now put the matrix A on the stack:
{ { 1 -1 } { 2 4 } }
After calling LDEC, we get:
At level 2, we have
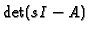 (with s=X):
(with s=X):
and level 3 is the comatrix of sI-A:
Level 2 and 3 will be useful if we want
to compute the solution of the LDEC with non-zero initial data , e.g.
y1(0)=1, y2(0)=2. If we look at Equation (1), we see
that we have to add
![${\cal L}^{-1}\left[ (sI-A)^{-1} y(0) \right] $](img122.gif) to the previous solution. To do this, type
to the previous solution. To do this, type { 1 2 },
multiply by the comatrix from level 3,
multiply by the inverse of the determinant from level 2
(you can note divide a vector, you must first invert the determinant
and then multiply):
call ILAP:
(4e2x-3e3x, -4e2x+6e3x )
and add the result to the previous solution:




Next: First order equations.
Up: Linear differential equations (systems)
Previous: Inverse laplace transform.
Bernard Parisse
1998-07-31