![]()
where M denotes the minimal polynomial of A
DIAG returns 7 levels:
![]()
where M denotes the minimal polynomial of A
Examples:
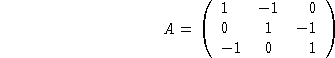
returns:
7: 0
6: { { '1/0' '1/0' '1/0' }
{ '1/0' '1/0' '1/0' }
{ '1/0' '1/0' '1/0' } }
5: { [[1 0 0] [[-2 -1 0] [[1 1 1]
[0 1 0] [0 -2 -1] [1 1 1]
[0 0 1] [-1 0 -2]] [1 1 1]] }
4: {1 -3 3 0}
3: {1 -3 3 0}
2: { :0: {1 1 1}
:<<(3,0)/2 (0,1)/2 3>>: {1 '(-1,0)/2+(0,-1)/2*V3' '(-1,0)/2+(0,1)/2*V3'}
:<< (3,0)/2 (0,-1)/2 3>>: {1 '(-1,0)/2+(0,1)/2*V3' '(-1,0)/2+(0,-1)/2*V3'}
1: {0 1 '(3,0)/2+(0,1)/2*V3' 1 '(3,0)/2+(0,1)/2*V3' 1 }
This means that A has 3 eigenvalues ![]()
corresponding to ![]() .
The characteristic and minimal polynomial are identical
(this is generically the case) X3-3X2+3X. The matrix is not
invertible (
.
The characteristic and minimal polynomial are identical
(this is generically the case) X3-3X2+3X. The matrix is not
invertible ('1/0' is infinite) and has a 0 determinant.
7: 1
6: { { 1 0 } { 0 1 } }
5: { [[1 0]
[0 1]] }
4: {1 -2 1}
3: {1 -1}
1: { :1, Eigen: { 0 1 } :1, Eigen: { 1 0 } }
2: {1 2}
The minimal polynomial is X-1, different form the characteristic polynomial
(X-1)2=X2-2X+1.

{ { 1 A }
{ A 1 } }
MAD, factor the characteristic
polynomial (e.g. by trying the FCTR instruction of ALG48)
before calling DIAG. If you have ALG48 installed, try e.g.
{ { 1 1 X }
{ 1 X 1 }
{ X 1 1 } }
MAD FCTR DIAG
Note that this example is solved by typing DIAG directly but it may
fail in other situations.
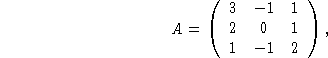
returns:
7: -4
6: : { { '1/4' '1/4' '-1/4' }
{ '-3/4' '5/4' '-1/4' }
{ '-1/2' '1/2' '1/2' } }
5: { [[ 1 0 0] [[ -2 -1 1] [[ 1 1 -1]
[ 0 1 0] [ 2 -5 1] [-3 5 -1]
[ 0 0 1]] [ 1 -1 -3]] [-2 2 2]] }
4: {1 -5 8 -4}
3: {1 -5 8 -4}
2: { :2, Char: { 2 2 1 } :2, Eigen:{ 1 1 0 } :1: { 0 1 1 } }
1: { 2 2 1 1}
This means that 2 has multiplicity 2, but the corresponding eigenspace
is only 1-dimensional
(spanned by (1,1,0) the last vector of the Jordan chain). The first
vector (2,2,1) is only a characteristic vector, his image by (A-2I)
is the eigenvector (1,1,0) .