Réduction des matrices par l'algorithme du pivot partiel.

  Pour réduire une matrice, entrez la matrice sur le niveau 1 de la pile (si la matrice ne contient pas de paramètres, vous pouvez utiliser MatrixWriter, sinon il faut rentrer une liste de listes, en d'autres termes remplacer les crochets [] par des accolades {}) puis lancez le programme RED.

Vous avez alors le choix entre RED qui crée des 0 de part et d'autre de la diagonale ou RANG qui crée des 0 sous la diagonale. Attention: le programme considère que la dernière colonne est une colonne de constantes (2ème membre d'un système par exemple), et ne crée pas de 0 dans cette colonne. Si nécessaire, ajoutez une colonne de zéros!

Si le flag 1 est armé, les étapes intermédiaires de la réduction sont affichées, l'utilisateur doit appuyer sur CONT (la touche-menu en haut à droite) à chaque étape. Il peut également interrompre la réduction en tapant HALT par exemple pour visualiser complètement une grande matrice. La reprise du programme s'effectue alors par (la touche en bas du clavier).

Le pivot choisi est l'élément du reste de la colonne dont le module est maximal. Par convention:

• un scalaire nul a comme module -8,
• un scalaire non nul a comme module sa valeur absolue lorsque le flag 15 est désarmé ou 1 pour un complexe et 2 pour un réel lorsque le flag 15 est armé,
• un identificateur global a pour module ,
• un algébrique ou une liste , où l est le nombre d'éléments de l'algébrique.

En mode symbolique (flag 15 armé), on limite ainsi les cas particuliers et on facilite leur résolution, alors qu'en mode numérique on minimise les erreurs d'arrondi (meilleure stabilité).

A la fin de la réduction, vous voyez au niveau 2 la liste des pivots. Chaque fois qu'un pivot de type symbolique s'annule, il faut reprendre la réduction dans ce cas particulier. Si vous savez résoudre l'équation pivot=0, rappelez la matrice originale sur la pile (tapez MATRIX) puis tapez une équation du type '<parametre>=valeur' puis L2S (ou -shift droit- en mode User) et enfin à nouveau RED.

Par exemple, supposons que l'on résolve le système:

Pour et , il y a une solution unique obtenue en tapant
{ {M 1 -2} { M 'M-1' 2 } }
puis RED RED qui donne au niveau 1:
{ { '-M^2+2*M' 0 '2*M' } { 0 '2-M' -4 } }.
C'est-à-dire que:

Au niveau 2 de la pile se trouvent la liste des pivots. Le pivot 'M^2+-2*M' s'annule lorsque m=2 et m=0 et on s'aperçoit qu'il n'y a pas d'autres cas particuliers. Pour réduire le système lorsque m=0 par exemple, rappelez la matrice au niveau 1 (en tapant MATRIX), puis tapez 'M=0' suivi de L2S (ou -shift- en mode user) puis relancez RED RED (on obtient ainsi x quelconque et y=-2). Pour le cas m=2, recommencez la même opération.

A noter que les sous-programmes SYST et SOLGEN sont prévus spécialement pour résoudre les systèmes linéaires. Au niveau 1 de la pile vous rajoutez la liste des variables et le coefficient multiplicateur de la colonne des coefficients constants (-1 si les coefficients constants sont à droite du signe ``=", 1 sinon). Vous obtenez alors les inconnues principales en fonction des inconnues auxiliaires et les équations de compatibilité sur les paramètres (attention, les inconnues auxiliaires peuvent ne pas apparaître dans l'expression des inconnues principales, mais la liste des inconnues au niveau 3 est ordonnée de la façon suivante: inconnues principales, inconnues auxiliaires, la coupure est faite par le terme 1 ou -1 s'il y a des termes constant sinon il faut comparer avec la liste originale). Par exemple, pour le système ci-dessus, le niveau 1 doit contenir {X Y -1} et le niveau 2 la matrice
{ {M 1 -2} {M 'M-1' 2} }
On obtient alors la solution unique du cas général:
{ :'X': '2/(-M+2)' :'Y': '4/(M+-2)' }
Ici, il n'y a pas d'inconnues auxiliaires (le niveau 2 contient { X Y -1} identique au niveau 3). Les cas particuliers sont au niveau 2. Pour m=0, on reprend la liste de variables et la matrice de départ (tapez MATRIX puis (non-shifté car il s'agit de décomposer la liste du niveau 1 en 2 listes) puis (pour SWAP) puis 'M=0' L2S et encore ), ce qui donne:

2: { { 0 1 -2} { 0 -1 2 } }
1: { X Y Z -1}

on tape enfin RED puis SYST et on obtient la solution générale:
{ :'Y': -2 }
donc les deux équations sont compatibles et y=-2. De plus au niveau 2, la liste des variables est {Y -1 X} donc x est une inconnue auxiliaire (en d'autres termes x est quelconque). En général les inconnues auxiliaires apparaissent dans l'expression des inconnues principales (ce n'est pas le cas ici). Pour m=2, on obtient:
{ :'X': '-1-1/2*Y' :-1: 0 }
donc les équations sont incompatibles car .

Vous pouvez aussi obtenir une représentation paramétrique de l'espace des solutions d'un système en tapant SOLGEN au lieu de SYST. Le niveau 1 contient alors la solution générale et les équations de compatibilité. Sur l'exemple précédent (m=0), on obtient ainsi au niveau 1:
If { }, { X Y }=: { X -2 }

L'option INVL de RED permet d'inverser une matrice carrée placée au niveau 1 de la pile. Son intérêt est d'inverser des matrices avec paramètres, fractions et racines carrées (à condition qu'il n'y ait pas trop de paramètres, sinon les calculs seront pénibles et longs),

Enfin, l'option DET de RED calcule le déterminant d'une matrice carrée par réduction. Ce qui permet parfois d'obtenir le déterminant sous forme factorisée, contrairement au programme DET qui renvoie toujours un résultat non factorisé. Vous pouvez naturellement poursuivre la factorisation en tapant COLC. Notez que le résutat peut avoir un dénominateur, dans ce cas utilisez EXPA pour le supprimer (parfois on peut aussi utiliser COLC suivi de COLCT).

Schémas de pile des programmes appelés par RED

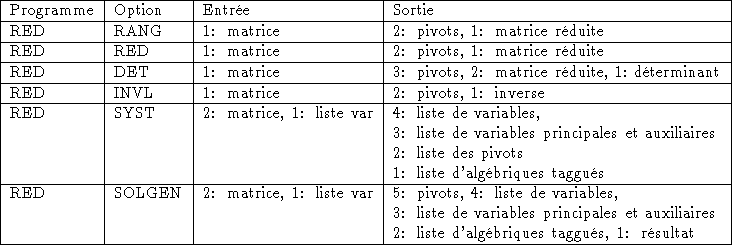
Quelques exemples d'utilisation:

• Réduire un système:

  Exemple:

  

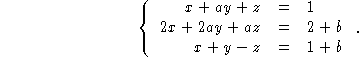
  Vous entrez sur la pile:
  { {1 A 1 1} {2 '2*A' A '2+B'} {1 1 -1 '1+B'} }
  puis vous tapez RED . Vous obtenez sur la pile:

  • au niveau 2, la liste des pivots,
    { 1 1 -1 'A-1' '-A+2' '-A+2' }
    ici le sytème est singulier si a=1 ou si a=2: il y a deux cas particuliers à étudier.
  • au niveau 1, la matrice réduite:

    { { '-A^2+3*A+2' 0 0 '(-A^2+A-1)*B+(-A^2+3*A-2)' }
      { 0 'A^2+-3*A+2' 0 '-A*B' }
      { 0 0 'A+-2' B } }

    donc le système admet une solution unique (si et ):

    

  Vous pouviez aussi taper { X Y Z -1} après la matrice de coefficients puis RED et enfin 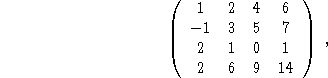ou .
• Pour déterminer le rang d'une matrice, par exemple:

  

  vous entrez les coefficients (par exemple avec MatrixWriter) puis vous tapez RED et , le rang est le nombre de coefficients diagonaux non nuls (ici 3).

• Même question mais avec un paramètre:
  { { 1 1 M } { 1 M 1 } { M 1 1 } } RED RANG
  La matrice réduite est:
  { { 1 1 M } { 0 '-1+M' '1-M' } { 0 0 '2-M-M^2' } }
  Au niveau 2, on voit un cas particulier m=1. Pour l'étudier, tapez simplement MATRIX puis 'M=1' puis L2S (ou -shift- en mode USER) et relancez RED .

  Essayez à nouveau cet exemple mais après avoir éteint l'indicateur 1 (1 CF) et comparez la vitesse d'exécution.

• Recherche de relations entre vecteurs.
  Supposons que l'on cherche à la fois le rang d'une famille et les relations linéaires entre les vecteurs v₁, v₂ et v₃. On rentre les coordonnées de v₁ en ligne suivie de V1, puis celles de v₂ suivies de V2 et enfin celles de v₃ suivies de V3 puis on tape RED . Si une ligne de coordonnées nulle apparaît, on a alors une relation linéaire entre les trois vecteurs (et le rang est le nombre de lignes non nulles). Par exemple si v₁(1,2,0), v₂(-2,-1,1), v₃(0,3,1), on entre:

  { { 1 2 0 V1 }
    { -2 -1 1 V2 }
    { 0 3 1 V3 } }

  puis RED, RANG et on obtient:

  { { 1 2 0 V1 }
    { 0 3 1 '2*V1+V2' }
    { 0 0 0 '-(2*V1)-V2+V3' } }

  donc la famille est de rang 2 et on a -2v₁-v₂+v₃=0.
• Calcul d'inverse par la méthode du pivot de Gauß .

  Exemple:

  { { '1/2' -1 }
    { 1    '2/3' } }
  RED INVL
  -> { { '1/2' '3/4'  }
       { '-3/4' '3/8' } }

• calcul d'un déterminant par réduction:

  { { 1 T T T }
    { 1 K T T }
    { 1 T K T }
    { 1 T T K } }
  RED DET -> '(-T+K)*(-T+K)*(-T+K)'

  Sur cet exemple particulièrement bien adapté, le déterminant est factorisé.