Définition
Un pavage c'est le remplissage du plan avec un motif sans
trous, sans chevauchements en utilisant
des isométries.
Une isométrie est une transformation qui conserve les longueurs,
les angles et les figures. Les translations, les rotations, les symétries
axiales et les symétries glissements sont les isométries
du plan.
Le pavé est la forme minimale que l'on peut transformer
pour couvrir le plan.
On ne peut pas utiliser n'importe quelle figure pour remplir le plan, les
principales figures
géométriques utilisées sont les quadrilatères,
les triangles, certains pentagones et hexagones.
Au contraire le pavage avec des heptagones réguliers n'est pas possible.
Les manières de paver :
Il y a 17 façons différentes de paver le
plan, avec des isométries dont 5 qui n'utilisent que des translations
et des rotations.
Des problèmes n'ont pas encore été résolus.
Les mathématiciens ont essayé de paver avec les 17 façons
en ne prenant qu'une seule figure géométrique. Par exemple
avec un pentagone ils n'ont trouvé que 14 familles pavant le plan.
D'autres manières de paver :
Différents jeux ou objets de la vie sont faits
grâce à des pavages : le jeu Tétris ou les tapisseries
avec des frises.
Dans la nature on peut retrouver des éléments composés
de pavages : les molécules et atomes,
les bulles de savon et les alvéoles dans les ruches d'abeilles.
Utilisation du pavage :
Les pavages peuvent servir dans plusieurs domaines :
* dans l'empaquetage par exemple dans les grandes surfaces pour ranger les
produits
(boîtes d'oeuf).
* dans la décoration (tissus, carrelage, églises, architecture).
* dans la couture (les patrons sont étudiés pour utiliser
le moins de tissus possible)...
Les démonstrations:
Pour être sur qu'un pavage peut couvrir le plan,
les scientifiques effectuent des démonstrations.
La seule transformation qui nous permet de dire qu'un pavage peut continuer
jusqu'à l'infini est
la translation.
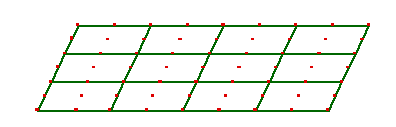
Voici le schéma d'une démonstration :
1) Dans un groupe de pavages il y a toujours deux familles
de translations de directions
différentes.
2) Avec un parallélogramme et deux translations on peut paver le
plan (pas besoin de rotations),
c'est le groupe R0.
3) Avec un parallélogramme et des rotations d'angle uniquement 180
on peut paver le plan,
c'est le groupe R2. Les centres de rotation sont disposés comme sur
la figure :
4) Les rotations d'un groupe de pavage ont des angles de mesure 360 /n (n
entier naturel).
5) Les centres de rotation ne sont pas disposés au hasard.
Si l'on a trois rotations R(A,360 /m), R(B,360 /n) et R(C,360 /p) de centres
respectifs les points A, B, C distincts et non alignés et d'angles
360 /m, 360 /n et 360 /p alors:
a) 1/m+1/n+1/p = 1
b) A, B, C sont disposés comme sur la figure :
6) Si un groupe de pavage contient une symètrie ou une symètrie
glissement alors elle contient forcément un des groupes précédents
( R0, R2, R3, R4, R6).
Voici les 17 façons de paver le plan
:
R0 : pas de rotation, uniquement des translations.
R2 : des rotations d'angle 180 .
R3 : des rotations d'angle 120 , 240 .
R4 : des rotations d'angle 90 , 180 .
R6 : des rotations d'angle 60 , 120 , etc...
M0 : pas de symétrie axiale, que des symétries glissement.
M0R2 : pas de symétrie axiale, des symétries glissement
et des rotations d'angle 180 .
M1 : une seule famille de symétries axiales.
M1g : une seule famille de symétries axiales et des symétries
glissement.
M1R2 : une seule famille de symétries axiales et des rotations
d'angle 180 .
M2 : deux familles de symétries axiales formant entre elles des
angles de 90 .
M2R2 : deux familles de symétries axiales formant entre elles
des angles de 90 et des rotations d'angle 180 .
M2R4 : deux familles de symétries axiales formant entre elles
des angles de 90 et des rotations d'angle 90 , 180 .
M3 : trois familles de symétries axiales formant entre elles des
angles de 60 .
M3R3 : trois familles de symétries axiales formant entre elles
des angles de 60 et des rotations d'angle 120 , 240 .
M4 : quatre familles de symétries axiales formant entre elles
des angles de 45 .
M6 : six familles de symétries axiales formant entre elles des
angles de 30 .
Voir aussi les sites web:
http://www-fourier.ujf-grenoble.fr/~bellinge/carreleur.html
http://www.mjc-andre.org