II) Les polyèdres réguliers

1) Les Solides Platoniciens

On connaît depuis l’Antiquité les cinq polyèdres réguliers appelés Solides Platoniciens.

Ces cinq solides peuvent être aisément réalisés à l’aide d’un patron. La formule d’Euler s’applique à ses polyèdres.

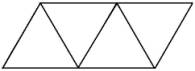
	Tétraèdre 4 faces (triangles équilatéraux) 4 sommets 6 arêtes
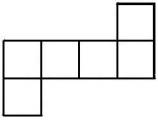
	Cube 6 faces (carrés) 8 sommets 12 arêtes
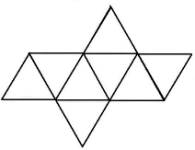
	Octaèdre 8 faces (triangles équilatéraux) 6 sommets 12 arêtes
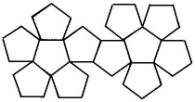
	Dodécaèdre 12 faces(pentagones réguliers) 20 sommets 30 arêtes
	Icosaèdre 20 faces (triangles équilatéraux) 12 sommets 30 arêtes

III) Les polyèdres réguliers non convexes

Johannes Kepler, a découvert en 1619 deux autres polyèdres réguliers non convexes : le petit dodécaèdre étoilé et le grand dodécaèdre étoilé. Deux siècles plus tard, en 1809 Louis Poinsot a découvert deux nouveaux polyèdres réguliers non convexes : le dodécaèdre étoilé et l’icosaèdre étoilé.

La formule d’Euler ne s’applique pas à ces polyèdres.

Le petit dodécaèdre étoilé	Le grand dodécaèdre étoilé
Le grand dodécaèdre	Le grand icosaèdre

IV) Réalisation des pièces élémentaires par pliage

1) Le dodécaèdre

Pour la construction du dodécaèdre, il faut réaliser 12 pièces identiques à la pièce élémentaire (2).

On remarque que chaque pièce est composée d’un pentagone régulier et de deux languettes.

(1) Faire un nœud simple avec une bande de papier de dimensions 41,7 cm par 5,5 cm.

(2) Tirer sur les extrémités afin de mettre à plat le nœud. Plier les bandes de papier qui dépassent pour former les languettes.

2) Les polyèdres réguliers à faces triangulaires

Pour la construction de ces solides on utilise la même pièce élémentaire A ou sa symétrique B. On remarque que cette pièce est composée de deux triangles équilatéraux situés au milieu de la pièce et de deux languettes. Lors du montage toutes les languettes doivent être utilisées.

Pièce A Pièce B

Réalisation de la pièce A

(1) Prendre une feuille de papier rectangulaire de dimensions L et L.	(2) Amener le sommet bas gauche sur le sommet haut droit. Plier.
(3) Plier le bas de la feuille en suivant le pli crée en (2).	(4) Plier le haut de la feuille en suivant le pli crée en (2).
(5) Plier les deux coins de façon à cacher les deux petits triangles rectangles qui dépassent sous les deux plis précédents.	(6) Retourner la pièce.
(7) Plier de façon à marquer les quatre triangles équilatéraux.	(8) Voici la pièce élémentaire finale A.

Réalisation de la pièce B

Prendre une feuille de papier rectangulaire de dimensions L et L.	(2) Amener le sommet bas droit sur le sommet haut gauche. Plier.
(3) Plier le bas de la feuille en suivant le pli crée en (2).	(4) Plier le haut de la feuille en suivant le pli crée en (2).
(5) Plier les deux coins de façon à cacher les deux petits triangles rectangles qui dépassent sous les deux plis précédents.	(6) Retourner la pièce.
(7) Plier de façon à marquer les quatre triangles équilatéraux.	(8) Voici la pièce élémentaire finale B.

3) Le cube

Pour la construction du cube, il faut réaliser six pièces identiques à la pièce élémentaire. On remarque que cette pièce est composée d’un carré et de deux languettes triangulaires. Lors du montage du cube toutes les languettes doivent être utilisées.

(1) Plier une feuille carrée en deux .	(2) Plier chaque bord sur la ligne médiane crée en (1) .
(3) Plier les deux petits triangles rectangles diagonalement opposés vers l’intérieur.	(4) Fermer le haut et le bas.
(5) Plier chaque coin bord à bord.	(6) Glisser les deux triangles formés en (5) vers l’intérieur.
(7)=>	Retourner la pièce. Plier les deux extrémités bord à bord pour former le carré du milieu et faire apparaître les deux languettes.

Attention la pièce symétrique (7’) à la pièce (7) est obtenue lorsqu’ en (3) on plie suivant l’autre diagonale du carré (figure (3’)). Le montage du cube nécessite des pièces parfaitement identiques.

(3’) (7’)

4) Nombre de pièces élémentaires nécessaires à la réalisation des polyèdres réguliers à face triangulaire

Tétraèdre	2 pièces symétriques (A+B)
Octaèdre	4 pièces identiques
Icosaèdre	10 pièces (5A+5B)
Petit dodécaèdre étoilé	30 pièces identiques
Grand dodécaèdre étoilé	30 pièces identiques
Dodécaèdre étoilé	35 pièces identiques
Icosaèdre étoilé	120 pièces identiques