S. Attal:  Open Quantum Random Walks

Abstract : We introduce a new model of quantum random walks which deals with density matrices instead of wave functions. These quantum random walks, called Open Quantum Random Walks, take into account the dissipative behavior of quantum systems in contact with an environment. We show that these OQRW contain all the classical Markov chains as a special case. We prove that despite their quantum character, from one step to the other, they converge to a more and more classical behavior as time goes.

10. J.Asch:  Some results on the Chalker Coddington model
    

Abstract: We consider the quantum network percolation model suggested by Chalker and Coddington to model the Quantum Hall Transition. We present some results concerning the localization regime.

Ch. Cedzich:  Quantum Walks in electric fields

Abstract: We explore the notion of discrete time counterparts of electric and

magnetic fields in the context of translationally invariant quantum walks on

the line. Comparisons with continuous time systems which exhibit a discrete

translational symmetry are drawn. As one does in such systems, we discuss

the difference of rational vs. irrational fields and discuss the impact of

rationality on properties of the quantum walks. In addition, concrete

recipies of how to electrify a quantum walk will be given.

K. Barr: Quantum Walks and Quantum Computation

Abstract: Both continuous and discrete time quantum walks are known to be universal for quantum computation. In this talk we discuss the computation with quantum walks in a variety of contexts. We will focus on discrete time quantum walks, and first outline how they can be used to simulate a universal gate set. Then we move onto examples of specific quantum walk algorithms. We conclude by introducing new work concerning quantum walks in terms of language acceptance. As the initial state of a quantum walk can be an arbitrary superposition, we develop the concept of a 'quantum input' and indicate how this work relates to the problem of state discrimination.  

A. Joye:  Spectral Transition for Random Quantum Walks on Trees

Abstract : We consider Random Quantum Walks describing the discrete time quantum dynamics of a particle with spin one (a three-state internal degree of freedom) hopping on the sites of the tree of degree 3. The deterministic Quantum Walks are characterized by a one step unitary evolution U(C) which first acts on the spin variables by means of unitary 3x3 matrix C and then makes the particle jump to its nearest neighbors on the tree by means of a spin-dependent shift. Decorating the matrix C with site-dependent random phases, one gets a Random Quantum Walk, characterized by the random unitary operator Uω(C). We investigate the spectral properties of Uω(C) as a function of C and exhibit spectral transitions along certain families of matrices C we describe. Joint work with Eman Hamza.

S. De Bièvre:  Scattering induced diffusion and current in a tight binding band

Abstract: In the single band tight-binding approximation, we consider the transport properties of an electron subject to a homogeneous static electric field. We show that repeated interactions of the electron with two-level systems in thermal equilibrium suppress the Bloch oscillations and induce a steady current, the statistical properties of which we study.

J. Roland: Quantum algorithms based on quantum walks

Abstract: In this talk, we will give a survey of quantum algorithms based on quantum walks, focusing in particular on search algorithms. The father of almost all quantum search algorithms is Grover's algorithm, which can be seen as a quantum walk on the complete graph. Later on, variations of Grover's algorithm have been proposed for searching on other graphs, such as the grid or the hypercube. Building on those ideas, Ambainis proposed a groundbreaking algorithm for the Element Distinctness problem, based on a quantum walk on the Johnson graph. Around the same time, Szegedy developed a general method to map a classical random walk to a quantum walk on the same graph. These works led to a flurry of results, including conceptual implications such as generic speedups of quantum walks over random walks, as well as concrete applications in the form of new quantum algorithms for various problems.

P. Arrighi:  Quantum Cellular Automata: structure, universality

Abstract: Quantum Walks can be generalized to have multiple walkers, which leads to Quantum Cellular Automata. We will see that another, more axiomatic route also leads to Quantum Cellular Automata, i.e that they can be characterized as mathematical objects via three natural properties: translation-invariance, unitarity, causality. We will show how very simple Walker-Walker interaction rules lead to a very powerful kind of universality.

N. Guillotin:  Introduction to random walk in random and non-random environments

Abstract: In this talk I will present some typical behaviors of random walks evolving in Z  .

The case of the random walks evolving in random environments will also be discussed.

d

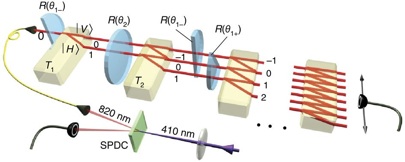
F. Sciarrino:  Quantum walk with integrated photonics

Abstract:    Integrated  photonic  circuits  have  a  strong potential  to  perform  quantum  information  processing  [1,  2].    Indeed,  the  ability  to  manipulate  quantum  states  of  light  by  integrated  devices  may  open  new  perspectives  both  for  fundamental  tests  of  quantum  mechanics  and  for novel  technological  applications  [3,4].  First we reported the realization of a directional coupler, fabricated by femtosecond laser waveguide writing, acting as an integrated beam splitter able to support polarization-encoded qubits [5]. Using this device, we demonstrate quantum interference with polarization-entangled states. Hence we demonstrated the first  integrated  photonic Controlled-NOT (CNOT) gate for polarization encoded qubits [6].

  As following step we addressed the implementation of quantum walk. This represents one of the most promising resources for the simulation of physical quantum systems, and has also emerged as an alternative to the standard circuit model for quantum computing. Up to now the experimental implementations have been restricted to single particle quantum walk, while very recently the quantum walks of two identical photons have been reported. For the first time, we investigated how the particle statistics, either bosonic or fermionic, influences a two-particle discrete quantum walk [7]. Such experiment has been realized by adopting two-photon entangled states and integrated photonic circuits.

  The following step has been to exploit this technology to simulate the evolution for disordered quantum systems. Waves fail to propagate in random media. First predicted for quantum particles in the presence of a disordered potential, Anderson localization has been observed also in classical acoustics, electro- magnetism and optics. Here, we report the observation of Anderson localization of pairs of entangled photons in a two-particle discrete quantum walk affected by position dependent disorder. A quantum walk on a disordered lattice is realized by an integrated array of interferometers fabricated in glass by femtosecond laser writing. Polarization entanglement is exploited to simulate the different symmetries of the two-walker system. We are thus able to experimentally investigate the genuine effect of bosonic and fermionic statistics in the absence of interaction between the particles. We will show how different types of randomness and the symmetry of the wave-function affect the localization of the entangled walkers.

References

[1]  T. D. Ladd, et al, “Quantum computers”,  Nature  464, 45–53 (2010).

[2] J. L. O’Brien, A. Furusawa, and J. Vuckovic,  “Photonic quantum technologies”, Nature Photonics  3,  687  (2009).

[3] P. Kok, et al, “Linear optical quantum computing with photonic qubits”, Rev. Mod. Phys. 79, 135 (2007).

[4] A. Politi, J. Matthews, M. Thompson, and J.O’Brien, “Integrated quantum photonics”, Selected Topics in Quantum Electronics, IEEE Journal of QE  1673, 15 (2009).

[5] L. Sansoni, F. Sciarrino, G. Vallone, P. Mataloni, A. Crespi, R. Ramponi, R. Osellame,  “Polarization entangled state measurement on a chip”, Phys. Rev. Lett. 105, 200503 (2010).

[6] A. Crespi, R. Ramponi, R. Osellame, L. Sansoni, I. Bongioanni F. Sciarrino, G. Vallone, P. Mataloni, “Integrated photonics quantum gates for polarization qubits”, Nat. Commun. 2:566 (2011)

[7] L. Sansoni, F. Sciarrino, G. Vallone, P. Mataloni, A. Crespi, R. Ramponi, R. Osellame, “Two-particle bosonic-fermionic quantum walk via 3D integrated photonics”, Phys. Rev. Lett. 108, 010502 (2012).

20. T.Rybar:  Index of quantum cellular automata, application to strictly forgetful memory channels
    

Abstract: We show that every automorphic memory channel T with finite depth (thus a quantum cellular automaton) needs a memory overhead of dimension ind T, where ind T is a local property of T known as the index of the quantum cellular automaton [1]. An explicit construction of the corresponding collision model is also provided.

References:

[1]: D. Gross, V. Nesme, H. Vogts, and R. Werner; Index theory of one dimensional quantum walks and cellular automata

V. Nesme : Quantum Walks and Filter Banks

Abstract: From the world of signal processing, I bring to you the so-called paraunitary filter bank.  Unbeknownst to most researchers in our field, there is an formal equivalence between this object and the reversible quantum walk. I will illustrate this point by showing how papers written by the signal processing community thirty years ago can help us solve topical questions about the index theory of quantum walks.