MATHEMATISCHES
FORSCHUNGSINSTITUT
OBERWOLFACH
Miniworkshop:
Dynamics of Nonlinear Waves
January 19th -
January 25th, 2003
Abstracts
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Symplectic structure of t...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img1.gif)
The aim of this talk was to give an informal introduction to the
linear stability analysis of solitary wave solutions of Hamiltonian PDEs
using the Evans function. The backbone of the analysis is the
multi-symplectic representation of Hamiltonian PDEs. The talk began
with an introduction to multisymplecticity. Then, the implications of
this structure for the existence and linear stability problem was
presented. The Evans function was shown to have a geometric
representation, in terms of the determinant of a matrix of restricted
symplectic forms. A geometric instability condition was presented, and
the theory illustrated by application to a 2-parameter family of
solitary waves of the Boussinesq equation. An introduction to the
implications of multisymplecticity for two (and more) space dimensions
was also given. An application of the 2+1-dimensional case is to the
transverse instability of solitary waves. Other applications such as
symplectic structure of soliton interaction (for example in the
Zakharov-Kuznetsov equation), analyticity of the symplectic Evans
function, the potential role of the Maslov index, extension to infinite
dimensions of the symplectic Evans function, solitary waves of
Hamiltonian PDEs on manifolds and other potential open problems were
also briefly discussed.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Destabilization of fronts...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img2.gif)
We consider a class of bi-stable reaction-diffusion equations in two
components on the real line. We assume that the system is
singularly perturbed, i.e. that the ratio of the diffusion
coefficients is (asymptotically) small. This class admits front
solutions that are asymptotically close to the (stable) front
solution of the `trivial' scalar bi-stable limit system
ut = uxx + u(1-u2). However, in the system these fronts
can become unstable by varying parameters. This destabilization
is either caused by the essential spectrum associated to the
linearized stability problem, or by an eigenvalue that
exists near the essential spectrum. We use the Evans function
to study the various
bifurcation mechanisms and establish an explicit connection between the
character of the destabilization and the possible appearance of
saddle-node bifurcations of heteroclinic orbits in the existence
problem.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Dynamics of pulse-like
lo...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img3.gif)
I propose a new type of Billiard problem in which
angles of incidence and reflection are different.
This problem comes from the dynamics of pulse-like
localized patterns in R-D systems in 2D. In fact,
a system of 3-components possesses a moving pulse-
like localized solution which moves with constant velocity and
constant shape. It is called "a traveling spot solution".
The ODE which describes the motion of a traveling spot
is given in mathematically rigorous way under some
assumptions. Moreover, the case that there exist
multi-traveling spot solutions in R2 are also
treated. As the consequence, they interact repulsively
each other.
Next, we consider the motion of one traveling spot
in some region with Neumann boundary conditions. Then,
a traveling spot reflect from the boundary. In the
reflection, the angle of incidence is larger than
the angle of reflection, which gives a new type
of Billiard problem. If the region is a square,
there exists a stable limit cycle of orbit.
On the other hand, if we consider a rectangle
with the ratio L/M and change it, some
chaotic orbit which almost fills the region
appears. We also give a picture of the global structure
of the orbits with respect to the ratio by numerics.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Stability of modulated fr...
...llskipamount]
(joint work with Guido Schneider, Hannes Uecker)
}
\end{center}}$](img4.gif)
When the steady states at infinity become unstable through a
pattern forming bifurcation, a travelling wave may bifurcate
into a modulated front which is time-periodic in a moving
frame. This scenario has been studied by B. Sandstede and A. Scheel
for a class of reaction-diffusion systems on the real line.
Under general assumptions, they showed that the modulated
fronts exist and are spectrally stable near the bifurcation
point. I present here a model problem for which one can prove
the nonlinear stability of these solutions with respect to small
localized perturbations. This result does not follow from the spectral
stability, because the linearized operator around the modulated front
has essential spectrum up to the imaginary axis.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Mathematical modelling an...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img5.gif)
The classical model for subsonic flame fronts in
diffusive gaseous mixtures under the assumption of simple chemistry
is formulated as a free boundary problem for temperature and fuel concentration.
The reaction takes place at the free boundary which is moving into
the fresh zone leaving the burnt region behind. Mass flux going
into the flame is balanced by heat flux coming out of the
flame and is given by a temperature dependent reaction rate.
If the mixture contains dust, a radiation effect has to be taken
into account which has a nonlocal effect on the temperature equation.
Modelling the radiative flux by the Eddington equation of astrophysics,
we find that the flame front temperature is enhanced to values well above the
adiabatic temperature. The presence of dust makes the medium more flammable.
This model has been suggested by both Joulin and Buckmaster.
Our goal is to obtain a complete bifurcation and stability picture of travelling waves
in terms of the temperature and fuel concentration far away ahead of the flame,
and the relevant parameters in the model. These are, after some normalisations,
the Lewis number, the opacity, the Boltzmann number and the
Zel'dovich number.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{A Morse Index Theorem for...
...Deng}{}}{}
{
\\ [\smallskipamount]
(joint work with Jian Deng)
}
\end{center}}$](img6.gif)
It has been a long standing issue to relate the structure of a solution
of an elliptic boundary value problem with its degree of instability,
i.e. its Morse Index. In one dimension, this is easily achieved using
Sturm-Liouville theory which affords a relationship between the number
of sign-changes of the derivative of the solution with its Morse Index.
A generalization of this idea to systems of elliptic equations with a
gradient nonlinearity is known and based on the idea that the
linearization of the system generates a flow on the space of Lagrangian
planes. This is closely related to the Morse Index Theorem which was
originally formulated for geodesics on a Riemannian manifold. We prove a
result of a similar structure but for solutions of elliptic problems in
arbitrary space dimensions, as long as the underlying domain is
start-shaped. The shrinking of the domain supplies the parameter that
renders a curve of Lagrangian subspaces from the linearization. The key
is to view these subspaces as lying in a Fredholm Lagrangian of
infinite-dimensional subspaces and develop a Maslov Index theory. The
result generalizes earlier work of Smale to now cover more general
boundary conditions and explains why Smale's result only worked for
Dirichlet conditions.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Semi-strong interaction
o...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img7.gif)
Pulse-pulse interactions
play central roles
in a variety
of pattern formation phenomena,
including self-replication.
In this talk,
we present
theory for the semi-strong interaction
of pulses
in a class of
singularly perturbed,
coupled reaction-diffusion equations
that includes the
(generalized) Gierer-Meinhardt,
Gray-Scott,
Schnakenberg,
and Thomas models,
among others.
Geometric conditions
are determined
on the reaction kinetics
for whether the pulses
in a two-pulse solution
attract or repel,
and ordinary differential equations
are derived
for the time-dependent separation distance
between their centers
and for their wave speeds.
In addition,
conditions
for the existence
of stationary two-pulse solutions
are identified,
and the interactions
between stationary and
dynamically-evolving
two-pulse solutions
are studied.
The theoretical results
are illustrated on
a series of examples.
In two of these,
which are related to
the classical Gierer-Meinhardt equation,
we find
that the pulse amplitudes blow up
in finite time. Moreover,
the blowup of stationary
one-pulse solutions
and of dynamically-varying two-pulse solutions
occurs precisely at the parameter values
for which the theory we develop
predicts that these solutions
should cease to exist.
Finally,
for one of these examples,
we discover a new type of codimension two point
in which the bifurcation curve of pulse-splitting
and the bifurcation curve of blowup intersect.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Evans' function for infin...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img8.gif)
The aim of the talk is to illustrate the construction of
Evans' function in infinite-dimensional setting.
The classical Evans' function was defined to be the determinant of
solutions which decay in plus or minus infinity. Several way of
defining Evans' function have been used which depend on some finite
dimensionality of each infinite dimensional system.
In this talk, a new definition of Evans' function is introduced,
which depends on Fredholm property of the system rather than
infinite dimensionality. The function is defined to be an analytic
section to the pull back of the determinant bundle over the space
of Fredholm operators. The multiplicity lemma and winding number
argument can also be shown in general framework.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Scattering dynamics in di...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img9.gif)
Scattering of particle-like patterns in dissipative systems is studied,
especially we focus on the issue how the input-output relation is controlled
at a head-on collision in 1D and 2D spaces where traveling pulses and spots
collapse. It remains an
open problem due to the large deformation of
patterns at a colliding point. We found that special type of steady or
time-periodic
solutions called separators and their stable and unstable manifolds direct
the traffic flow of orbits.
Such separators are clearly visible at a transition point
where the input-output relation is qualitatively changed such as from
annihilation to repulsion as parameters vary.
Separators are in general highly unstable which causes a variety of
input-output relations during the process of scattering.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Coherent Manifolds for Da...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img10.gif)
The interaction of light with matter is dominated by diffraction
and dispersion, absorption and stimulated emission all combining to
produce a noisy background of radiation. Against this background, certain
localized structures display a remarkable coherence through a robust
balancing of nonlinearity against forcing and dispersion. The emerging
technology of modern optics seeks to control these coherent structures for
purposes of data propagation, pattern generation, and optical logic.
From these coherent localized structures we iteratively build up a coherent manifold:
a low-dimensional, invariant manifold which captures the salient dynamics of
pulse interaction, bifurcation of fixed points and traveling waves,
oscillatory instabilities and modulation of multi-dimensional fronts.
The manifold is a sum of a base 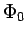 describing a
collection of localized coherent structures, and two small extensions,
describing a
collection of localized coherent structures, and two small extensions,
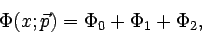 |
(1) |
where 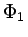 lies in a finite dimensional subspace and serves to extend
the dimension of the tangent plane of the manifold, and
lies in a finite dimensional subspace and serves to extend
the dimension of the tangent plane of the manifold, and 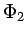 ,
the
radiative extension, lies in the large, complementary subspace and
is chosen to enforce the invariance or quasi-invariance of the manifold,
capturing radiative effects arising from the interplay between forcing and
damped dispersion. The manifold coordinates
,
the
radiative extension, lies in the large, complementary subspace and
is chosen to enforce the invariance or quasi-invariance of the manifold,
capturing radiative effects arising from the interplay between forcing and
damped dispersion. The manifold coordinates 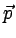 represent slow modes of
the system and are typically identified with localized eigenmodes of the
linearization
represent slow modes of
the system and are typically identified with localized eigenmodes of the
linearization
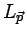 of the vector field about
of the vector field about
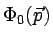 .
These eigenmodes
arise, for example, from symmetries or self-similar scalings of the PDE, and are
the ``free'' coordinates: position, phase, polarization, which
describe the state of the coherent structures.
.
These eigenmodes
arise, for example, from symmetries or self-similar scalings of the PDE, and are
the ``free'' coordinates: position, phase, polarization, which
describe the state of the coherent structures.
The construction is based upon
| (1) |
Detailed analysis of families of linearized operators by |
| |
Evans function and non-perturbative Krein-signature methods |
(2) |
Development of decay estimates for time-dependent semi-groups |
| |
via renormalization group methods. |
As a pro-typical optical system we consider the optical parametric oscillator
(OPO) which has attracted recent attention
as a source of broadly-tunable coherent radiation for use in pattern recognition technologies,
optical information processing, and infrared spectroscopy.
OPOs exploit the quadratic
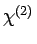 -nonlinearity of a non-centrosymmetric crystal
such as lithium niobate to convert energy parametrically from one frequency to
another. The development of quasi-phase matching (QPM) through periodic poling of the crystal's
molecular structure has has greatly increased the viability and
simplified the control of these devices while extending their operational
range and possible applications.
In a continuous pumping limit, the OPO process converts a coherent pump field V
into a frequency shifted signal field U, governed by the equations
in 1+2 dimensions,
-nonlinearity of a non-centrosymmetric crystal
such as lithium niobate to convert energy parametrically from one frequency to
another. The development of quasi-phase matching (QPM) through periodic poling of the crystal's
molecular structure has has greatly increased the viability and
simplified the control of these devices while extending their operational
range and possible applications.
In a continuous pumping limit, the OPO process converts a coherent pump field V
into a frequency shifted signal field U, governed by the equations
in 1+2 dimensions,
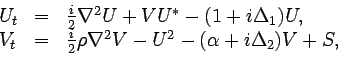 |
(2) |
where 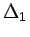 and
and 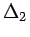 are the cavity detuning parameters and S
is a spatially dependent pump strength.
are the cavity detuning parameters and S
is a spatially dependent pump strength.
We examine pulse-pulse interactions for the OPO system, and describe a snaking-bifurcation
which results in multi-pulses. In the second talk we extend the method to consider
oscillatory pulses and the generation of stable periodic solutions and address
pattern formation in the context of multi-dimensional fronts.
![% latex2html id marker 732
$\textstyle \parbox{\textwidth}{ \begin{center}\textb...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img22.gif)
We study the
singular limit of a reaction-diffusion system known, in the engineering literature, as the thermo-diffusive model for flame propagation with one-step chemisty. The unknowns are the temperature and
the mass fraction of the reactant. There is a diffusivity ratio - the Lewis number, denoted by Le - which is usually taken equal to unity in the mathematical literature on this system. The parameter that makes the system singular is the inverse of the high activation energy 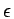 ,
which makes the reaction term converge - at least formally - to a measure on the surface where the temperature reaches its maximum value as
,
which makes the reaction term converge - at least formally - to a measure on the surface where the temperature reaches its maximum value as
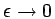 .
.
In the present context, 3D spherical symmetry is assumed, and the surface of maximal temperature is a sphere whose radius (flame radius) has an evolution law to be determined. We prove, under the assumption Le<1,
the existence of a class of initial data such that, for the solution starting from these data:
- the correct time scale is
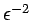 ,
,
- the the flame radius, after a rescaling in time, converges as
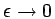 to the solution of a nonlinear integro-differential equation.
to the solution of a nonlinear integro-differential equation.
Such an equation had been derived by G. Joulin in 1985, but only in the formal style (matched asymptotic expansions).
The present paper gives a completely rigorous justification on Joulin's analysis; the method of proof is basically in two steps.
- The construction of an approximate solution to sufficiently high order in
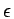 .
.
- Checking that the true solution is close enough to the approximate one; this involves sharp resolvent and semigroup estimates.
An important open problem is the study of the system on times scales
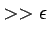 .
.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Stability of large Ekman ...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img28.gif)
We study the limit of the Navier-Stokes equation for an incompressible
three dimensional
rotating fluid when the Ekman and Rossby number go to zero. Near
horizontal boundaries an Ekman layer appears and its stability can
be characterized with a Reynolds number. For large Reynolds numbers,
the Ekman layer is known to be linearly unstable whereas
for very small Reynolds
numbers, the stability can be proved by classical energy estimates.
Here, we study the stability for intermediate Reynolds numbers by means
of Evans function/Symmetrizer's construction techniques.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Defects in oscillatory
m...
...el}{}}{}
{
\\ [\smallskipamount]
(joint work with Arnd Scheel)
}
\end{center}}$](img29.gif)
Among the many patterns that have been observed in experiments and
numerical simulations are defects. Defects are modulated waves that
are time periodic in an appropriate moving frame and asymptotic in
space to wave trains. In this talk, we show that spatial dynamics can
be used to analyse defects and their spectral stability properties. It
appears as if there are four different types of defects that are
robust: sinks, sources, transmission and contact defects. The
different defect classes are distinguished by their codimension and
the characteristic curves associated with them. Spatial dynamics also
allows us to determine the PDE spectrum of defects near the origin in
L2 and exponentially weighted L2 norms. The analysis of the
spectrum of contact defects is particularly involved and requires an
extension of the Evans function in situations where the Gap Lemma fails.
Open problems include a complete classification of defects, the
nonlinear stability of sources, transmission and contact defects,
bifurcations from and of defects, and finally their interaction
properties.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Extending the Evans funct...
...{
\\ [\smallskipamount]
(joint work with Bj\uml orn Sandstede)
}
\end{center}}$](img30.gif)
Contact defects arise in open classes of reaction diffusion
systems. Like other types of defects they are time-periodic in a
suitably comoving frame and spatially asymptotic to nonlinear wave
trains. Their characteristic feature is that the wavenumbers to the
left and to the right of the defect coincide, and that the speed of
propagation of the defect is given by the group velocity of the wave
trains in the far field. We are interested in stability, interaction,
and bifurcation properties of these types of defects. We therefore
investigate spectral properties of the linearization at the defect, in
a neighborhood of the origin, 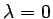 .
The fact that the speed of
propagation is given by the group velocity leads to two
difficulties. First, the convergence of the defect to the asymptotic
wave trains is only algebraic,
.
The fact that the speed of
propagation is given by the group velocity leads to two
difficulties. First, the convergence of the defect to the asymptotic
wave trains is only algebraic, 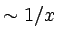 ,
and then
,
and then 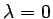 is a
branch point in the essential spectrum of the defect. In order to
characterize spectral properties, we construct an Evans function for
the ill-posed modulated wave equation, using first Galerkin
approximations globally in
is a
branch point in the essential spectrum of the defect. In order to
characterize spectral properties, we construct an Evans function for
the ill-posed modulated wave equation, using first Galerkin
approximations globally in 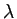 ,
and then center-manifold and
Lyapunov-Schmidt reduction, locally near
,
and then center-manifold and
Lyapunov-Schmidt reduction, locally near 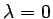 .
For the actual
construction of the Evans function, we use geometric blow-up and
resonant normal forms for the differential equation on the reduced
Grassmannian. As a main result, we show that the Evans function E
can be written as
.
For the actual
construction of the Evans function, we use geometric blow-up and
resonant normal forms for the differential equation on the reduced
Grassmannian. As a main result, we show that the Evans function E
can be written as
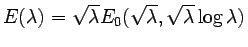 ,
where
,
where
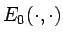 is
is 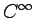 .
Moreover,
.
Moreover,
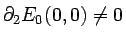 whenever the decay towards the wavetrains is of the
form
whenever the decay towards the wavetrains is of the
form
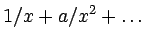 with
with 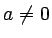 .
We also show that a similar
construction can be employed to continue the Evans function beyond the
Gap Lemma as a meromorphic function. Resonances between the
exponential decay of the wave profile and the gap between the leading
eigenvalues generate poles in the Evans function.
.
We also show that a similar
construction can be employed to continue the Evans function beyond the
Gap Lemma as a meromorphic function. Resonances between the
exponential decay of the wave profile and the gap between the leading
eigenvalues generate poles in the Evans function.

We consider solutions bifurcating from a spatially homogeneous equilibrium
under the assumption that the associated linearization
possesses continuous spectrum up to the imaginary axis,
for all values of the bifurcation parameter, and that a pair of imaginary eigenvalues
crosses the imaginary axis. For a reaction-diffusion-convection system
we investigate the nonlinear stability of the trivial solution
with respect to spatially localized perturbations, prove the occurrence
of a Hopf bifurcation and the nonlinear stability of the bifurcating time-periodic solutions,
again with respect to spatially localized perturbations.
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{The small viscosity limit...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img41.gif)
Starting with a curved multiD shock solution to a hyperbolic system
of conservation laws, we show how to obtain it as a limit as viscosity
goes to zero of smooth solutions to an associated parabolic (hyperbolic
+ viscosity) problem. We first construct the viscous boundary layer on
each side of the shock to high order (i.e., an approximate solution).
The leading term in the boundary layer expansion is given by a family
of travelling waves connecting endstates given by the original shock,
and the problem reduces to proving nonlinear stability of this family.
This is accomplished by proving L2 estimates for the parabolic
problem linearized about the approximate solution. A key step is to
remove
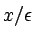 dependence from the coefficients of this problem by
an argument that combines the Gap Lemma with pseudodifferential
operators. One is then in a position to prove linear estimates using
Kreiss-type symmetrizers, and these estimates suffice to yield nonlinear
stability.
dependence from the coefficients of this problem by
an argument that combines the Gap Lemma with pseudodifferential
operators. One is then in a position to prove linear estimates using
Kreiss-type symmetrizers, and these estimates suffice to yield nonlinear
stability.
List of participants
THOMAS BRIDGES,
Department of Mathematics and Statistics,
School of ECM,
University of Surrey,
Guildford, Surrey,
GU2 5XH, UK,
t.bridges@surrey.ac.uk
ARJEN DOELMAN,
Korteweg-de Vries Institute,
Faculty of Sciences,
University of Amsterdam,
Plantage Muidergracht 24,
1018 TV Amsterdam,
the Netherlands,
doelman@science.uva.nl
SHIN-ICHIRO EI,
Graduate School of Integrated Science,
Yokohama City University,
22-2 Seto Kanazawa-ku,
Yokohama 236-0027, Japan,
ei2s@yokohama-cu.ac.jp
THIERRY GALLAY,
Institut Fourier,
Université de Grenoble I,
BP 74,
38402 Saint-Martin d'Hères,
France,
Thierry.Gallay@ujf-grenoble.fr
JOOST HULSHOF,
Department of Mathematics,
Faculty of Sciences,
Vrije Universiteit,
De Boelelaan 1081a,
1081 HV Amsterdam,
The Netherlands,
jhulshof@cs.vu.nl
CHRISTOPHER JONES,
Mathematics Department,
University of North Carolina,
Chapel Hill, NC 27599, USA,
ckrtj@amath.unc.edu
TASSO KAPER,
Department of Mathematics
and Center for BioDynamics,
Boston University,
111 Cummington Street,
Boston, MA 02215, U.S.A.
tasso@math.bu.edu
SHUNSAKU NII,
Department of Mathematics,
Faculty of Science,
Saitama University,
255 Shimo-Okubo, Saitama 338-8570,
Japan,
snii@rimath.saitama-u.ac.jp
YASUMASA NISHIURA,
Laboratory of Nonlinear Studies and Computation,
Research Institute for Electronic Science,
Hokkaido University,
N12 W6 Sapporo,
060-0812, JAPAN,
nishiura@aurora.es.hokudai.ac.jp
KEITH PROMISLOW,
Simon Fraser University,
Dept. of Mathematics,
Burnaby BC, V5A 1S1,
Canada,
kpromisl@cs.sfu.ca
JEAN-MICHEL ROQUEJOFFRE,
Laboratoire MIP, UFR MIG,
Universite Paul Sabatier 118,
route de Narbonne, 31062 Toulouse,
Cedex, France,
roque@mip.ups-tlse.fr
FREDERIC ROUSSET,
Laboratoire J. A. Dieudonne,
U.M.R. C.N.R.S. N 6621,
E. D. P. Analyse Numerique,
Universite de Nice Sophia-Antipolis,
France,
frousset@math.unice.fr
BJÖRN SANDSTEDE,
Department of Mathematics,
Ohio State University,
231 West 18th Avenue,
Columbus, OH 43210, USA,
sandsted@math.ohio-state.edu
ARND SCHEEL,
U Minnesota, School of Mathematics,
206 Church St. S.E.,
Minneapolis, MN 55455, USA,
scheel@math.umn.edu
GUIDO SCHNEIDER,
Universtät Karlsruhe (TH),
Mathematisches Institut I,
D-76128 Karlsruhe,
Germany,
guido.schneider@mathematik.uni-karlsruhe.de
MARK WILLIAMS,
Department of Mathematics, CB 3250,
University of North Carolina,
Chapel Hill, NC 27599,
USA,
williams@math.unc.edu
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Symplectic structure of t...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img1.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Destabilization of fronts...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img2.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Dynamics of pulse-like
lo...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img3.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Stability of modulated fr...
...llskipamount]
(joint work with Guido Schneider, Hannes Uecker)
}
\end{center}}$](img4.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Mathematical modelling an...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img5.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{A Morse Index Theorem for...
...Deng}{}}{}
{
\\ [\smallskipamount]
(joint work with Jian Deng)
}
\end{center}}$](img6.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Semi-strong interaction
o...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img7.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Evans' function for infin...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img8.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Scattering dynamics in di...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img9.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Coherent Manifolds for Da...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img10.gif)
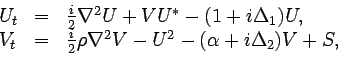
![% latex2html id marker 732
$\textstyle \parbox{\textwidth}{ \begin{center}\textb...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img22.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Stability of large Ekman ...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img28.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Defects in oscillatory
m...
...el}{}}{}
{
\\ [\smallskipamount]
(joint work with Arnd Scheel)
}
\end{center}}$](img29.gif)
![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{Extending the Evans funct...
...{
\\ [\smallskipamount]
(joint work with Bj\uml orn Sandstede)
}
\end{center}}$](img30.gif)

![$\textstyle \parbox{\textwidth}{ \begin{center}\textbf{The small viscosity limit...
...nelse{\equal{}{}}{}
{
\\ [\smallskipamount]
(joint work with )
}
\end{center}}$](img41.gif)