Pour mieux comprendre le comportement des ondes en milieu chaotique,
nous allons considérer un modèle de dynamique chaotique encore plus
simple.
- Comme la matrice est à coefficients entiers, le résultat obtenu sur
les parties fractionnaires de
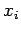 ,
,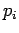 , ne dépend pas de
leur partie entière. On represente donc
, ne dépend pas de
leur partie entière. On represente donc
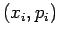 dans le domaine
dans le domaine
![$ \left[0,1\right]\times\left[0,1\right]$](img111.png) , appelé
tore
, appelé
tore
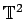 .
.
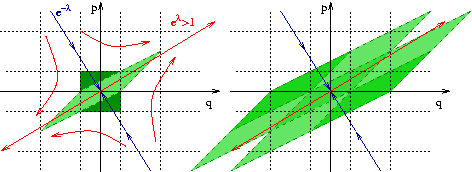
- Sur le tore
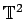 il résulte une dynamique chaotique
avec étirement dans la direction instable et ``repliement''
dans la direction stable.
il résulte une dynamique chaotique
avec étirement dans la direction instable et ``repliement''
dans la direction stable.
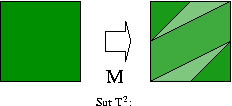
- En particulier les directions instables et stables issues de l'origine
ont une pente irrationnelle, et ``s'enroulent sur le tore'', en
formant un réseau dense.
![\includegraphics[%
scale=1.5]{varietes.eps}](img113.png)
- La dynamique est ``fortement chaotique'' avec les propriétés
d'être hyperbolique, ergodique et mélangeante.
Subsections
faure frederic
2003-09-12
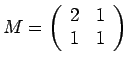 est d'étirer dans la direction instable (rouge) avec le
coeficient de Lyapounov
est d'étirer dans la direction instable (rouge) avec le
coeficient de Lyapounov
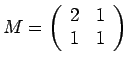 est d'étirer dans la direction instable (rouge) avec le
coeficient de Lyapounov
est d'étirer dans la direction instable (rouge) avec le
coeficient de Lyapounov


![\includegraphics[%
scale=1.5]{varietes.eps}](img113.png)