The good Christian should beware of mathematicians, and all those who make empty prophecies. The danger already exists that the
mathematicians have made a covenant with the devil to darken the spirit and to confine man in the bonds of Hell. (Saint Augustine).
De Genesi ad Litteram, Book II, xviii, 37

   Divertissements mathématiques...
 1)  Le ruban de Moebius

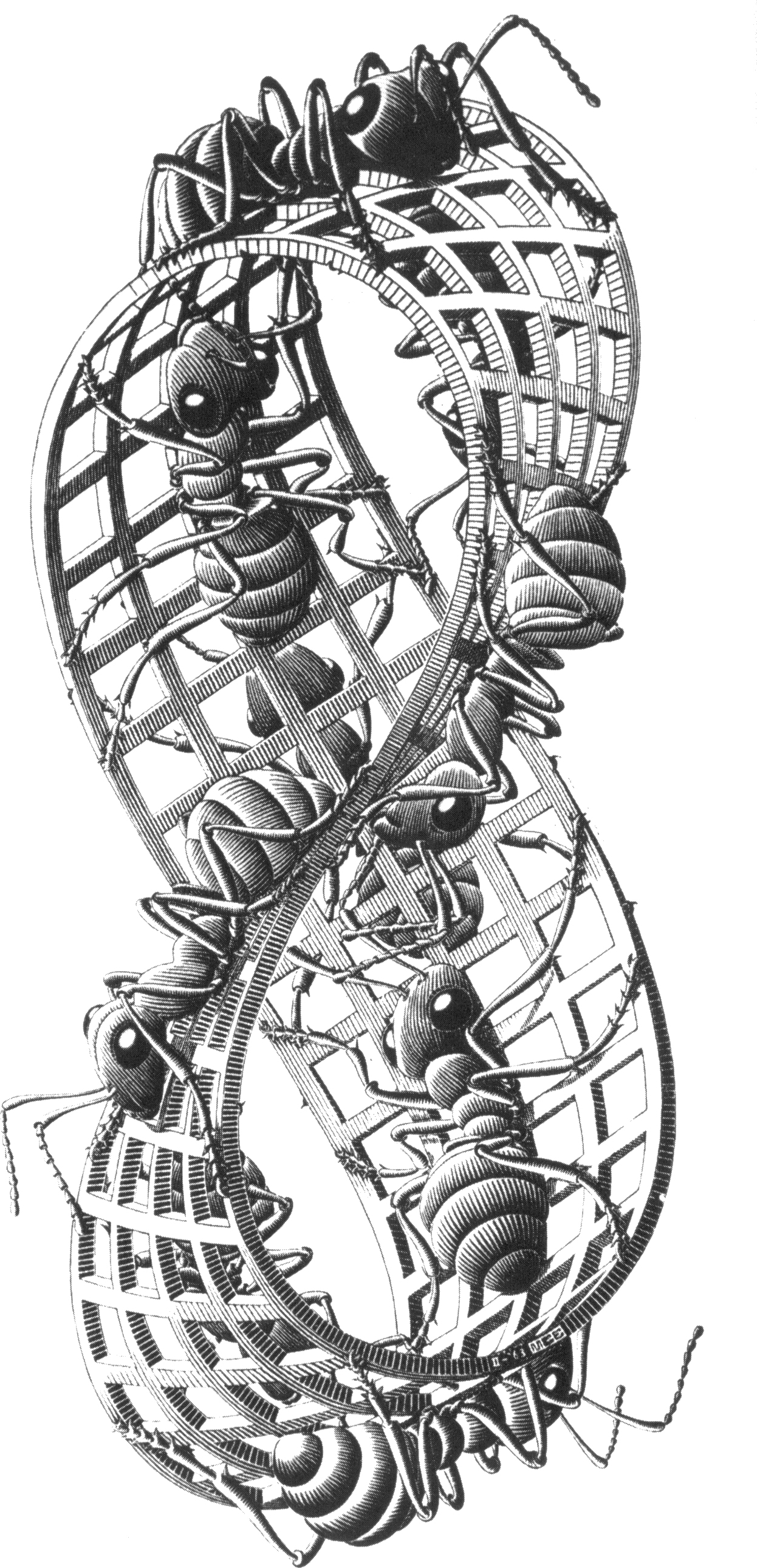
Celui-ci, je l'ai utilisé avec des gamins de sept ans comme avec des grand-pères de soixante-dix : ça plaît à tout le monde
(matheux confirmés qui l'ont vu 3567 fois déjà y compris mais surtout pour des raisons de nostalgie).

 C'est donc un ruban de papier dont on colle les deux bouts comme si on voulait faire un cercle, mais avant de les recoller,
 on y introduit une demi-torsion, crééant ainsi un objet avec des propriétés géométriques forts paradoxales. A essayer :

 découper un ruban de moebius le long de son milieu,
 redécouper le ruban qui en résulte,
 colorier un ruban de moebius rouge d'un côté et vert de l'autre,
 tracer le bord d'un ruban de moebius avec un stylo noir,
 découper un ruban de moebius le long  d'une courbe tracée parallèle au bord et proche de celui-ci...

 essayez avec des rubans avec deux demi-torsions, avec trois, avec quatre, faites des conjectures, testez-les, bref,
 éclatez vous.

                                                    (Celui qui trouve étrange l'idée de s'éclater avec un bout de papier, de la colle et des ciseaux est définitivement perdu pour la
                                                    science et devrait aller faire autre chose.)                    

A quoi ca sert?
  L'usage principale d'un ruban de Moebius est de permettre aux adultes de revivre l'étonnement qu'ils connurent jadis la veille de Noel en découvrant des cadeaux mystérieusement apparus à côté du sapin.

On peut aussi coller deux rubans de Moebius le long de leur (unique) bord pour fabriquer une bouteille de Klein
(voir à côté.) Suivre ce lien pour acheter (à un prix très raisonnable) une bouteille de Klein (ou simplement pour
rire un peu si vous appréciez l'humour matheux.)

Mais sérieusement?

       Bon, puisque vous insistez : le ruban de Moebius est l'exemple le plus simple qui soit d'une système dans lequel il faut faire deux tours complets avant de   
       revenir à son point de départ.

       Imaginez une formi qui marcherait sur un ruban de Moebius. Après avoir fait une tour complet la bête se retrouve à son point de départ... du mauvais côté du
       ruban. Il lui faudrait faire deux tours complets avant de revenir à son vrai point de départ. Pendant longtemps, nous crûmes que ce genre de comportement     
       n'était qu'une curiosité mathématique, mais nous ne prenions pas assez en compte le côté surréaliste de la physique moderne. 

"A prima vista nulla sembra assomigliare meno a Eudossia che il disegno del tappeto, ordinato in figure simmetriche che ripetono i loro motivi lungo linee rette e circolari, intessuto di gugliate dai colori splendenti, l'alternarsi delle cui trame puoi seguire lungo tutto l’ordito. Ma se ti fermi a osservarlo con attenzione, ti persuadi che a ogni luogo del tappeto corrisponde un luogo della città e che tutte le cose contenute nella città sono comprese nel disegno, disposte secondo i loro veri rapporti, qual sfuggono al tuo occhio distratto dall'andirivieni dal brulichio dal pigiapigia. Tutta la confusione di Eudossia, i ragli dei muli, le macchie di nerofumo, l'odore del pesce, è quanto appare nella prospettiva parziale che tu cogli; ma il tappeto prova che c'è un punto dal quale la città mostra le sue vere proporzioni, lo schema geometrico implicito in ogni suo minimo dettaglio. Ogni abitante di Eudossia confronta all'ordine immobile del tappeto una sua immagine della città, una sua angoscia, e ognuno può trovare nascosta tra gli arabeschi una risposta, il racconto della sua vita, le svolte del destino.

Sul rapporto misterioso di due oggetti così diversi fu interrogato un oracolo. Uno dei due oggetti, — fu il responso,— ha la forma che gli dei diedero al cielo stellato e alle orbite su cui ruotano i mondi; l'altro ne è un approssimativo riflesso, come ogni opera umana.

Gli àuguri già da tempo erano certi che l'armonico disegno del tappeto fosse di fattura divina; in questo senso fu interpretato l'oracolo, senza dar luogo a controversie. Ma allo stesso modo tu puoi trarne la conclusione opposta: che la vera mappa dell'universo sia la città d'Eudossia cosi com'è, una macchia che dilaga senza forma, con vie tutte a zigzag, case che franano una sull'altra nel polverone, incendi, urla nel buio."

Da Italo Calvino, Le città invisibili, Einaudi, Torino 1979, pp. 103-104.