Roland Bacher
started in september 04, last update: september 04
Under construction.
The aim of these notes is to present a few problems and conjectures
related to the my joint paper with R. Chapman
Symmetric Pascal matrices modulo ![]() (European J. of Combinatorics 25 (2004) 459-473).
(European J. of Combinatorics 25 (2004) 459-473).
Denote by ![]() the infinite symmetric matrix with coefficients
the infinite symmetric matrix with coefficients
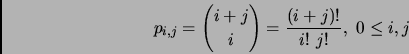

We denote by ![]() the symmetric
the symmetric ![]() submatrix of
submatrix of ![]() defined
by the
defined
by the ![]() first rows and columns. The matrix
first rows and columns. The matrix ![]() has thus coefficients
has thus coefficients
![]() with
with ![]() . Denote by
. Denote by
![]() the characteristic polynomial of
the characteristic polynomial of ![]() (where
(where ![]() denotes of course the identity matrix of order
denotes of course the identity matrix of order ![]() ).
).
The main result of [1] (Theorem 1.3 in [1]) reads now:
This result determines the reduction modulo ![]() of the
characteristic polynomial
of the
characteristic polynomial ![]() completely.
completely.
Theorem 0.1 seems to be the tip of an iceberg. Many similar formulae seem to exist. The easiest one (Conjecture 1.6 of [1]) can be stated as follows:
The equality
![]() states of course that the
polynomials
states of course that the
polynomials
![]() are palindromic:
are palindromic:
![]() and their roots are symmectric with
respect to the unit circle:
and their roots are symmectric with
respect to the unit circle:
![]() is a root of
is a root of ![]() if and
only if
if and
only if
![]() is a root of
is a root of ![]() .
.
The first few of these conjectural polynomials ![]() are seemingly
are seemingly
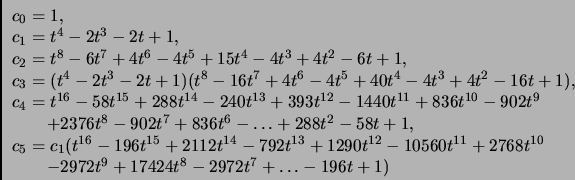
If this conjecture holds then
Computations with ![]() for
for ![]() suggest
(cf. Conjecture 1.7 in [1]):
suggest
(cf. Conjecture 1.7 in [1]):
Theorem 0.1 and Conjectures 0.2 and 0.3
define now ![]() completely modulo
completely modulo ![]() from the trivial
initial values
from the trivial
initial values ![]() and
and ![]() .
.
Proofs of these conjectures would thus be very interesting.