suivant: À propos de ce
monter: miastp7_2003
précédent: Avec la TI89/92
Exercice 1 (à rendre à la fin de la séance)
- Écrire S(x), le développement en
séries entières au voisinage de x = 0 de
f (x) = ln(1 + x2).
- Soit Sn(x) la somme partielle de la série S jusqu'à l'ordre
n (inclus).
Tracer sur un même graphique les graphes des fonctions f, S0,
S2 et S4.
- Graphiquement on voit que S4(x) approche f (x) : sur quel intervalle
cette approximation vous paraît-elle acceptable ?
- Donner une majoration de la valeur absolue du reste R4(x) de
cette série S(x) pour
x
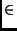 ] - 1, 1[.
Donner une majoration de
| f4(x) - f (x)| pour
x
] - 1, 1[.
Donner une majoration de
| f4(x) - f (x)| pour
x 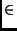 [- 1/4, 1/4]
indépendante de x.
En déduire un encadrement de ln(17/16).
[- 1/4, 1/4]
indépendante de x.
En déduire un encadrement de ln(17/16).
- On veut approcher sur l'intervalle [0;3/4]
f (x) à 10-3 près
par son développement en séries entières au voisinage de x = 0.
Déterminer le plus petit k pour que Sk(x) réalise cette
approximation sur cet intervalle. En déduire une valeur approchée
de
ln(25/16)
- On a
ln(25/16) = 2 ln(5/4). Donner un encadrement de
ln(5/4) en utilisant Sk pour la même valeur de k qu'à la
question précédente. En déduire une valeur approchée de
ln(25/16) et comparer avec la question précédente.
Exercice 2 (à rendre au début du TP8)
On veut calculer
I =
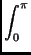
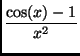 dx
dx
Écrire le développement en séries entières au voisinage de x = 0 de :
g(
x) =
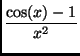
Écrire I sous la forme d'une série de terme général vj.
Soit Rn le reste de cette série :
Rn =
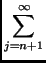 vj
vj
trouver une majoration de | Rn|.
Quelle est l'aproximation obtenue pour la valeur de I lorsqu'on utilise
comme approximation de
I, 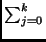 vj? Donner un encadrement
de I obtenu en prenant k = 10.
vj? Donner un encadrement
de I obtenu en prenant k = 10.



suivant: À propos de ce
monter: miastp7_2003
précédent: Avec la TI89/92
Bernard Parisse
2004-06-04
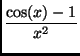 dx
dx