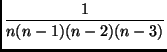
Exercice 1 (à rendre à la fin de la séance)
Déterminez à l'aide d'un logiciel un équivalent de
Exercice 2 (à rendre à la fin de la séance)
Ecrire un programme partiel_croi(f,N)
qui calcule la valeur approchée de la somme
partielle d'une série un = f (n) pour n variant de 1 à N
en effectuant la somme par valeur croissante de n,
et partiel_decr(f,N) par valeur décroissante de n.
Donnez les valeurs obtenues pour
f (x) = 1/x3, N = 104 et une précision
de 15 puis 30 digits. Comment expliquez-vous ces résultats?
Expliquez pourquoi si on calcule les
sommes partielles de la série de terme général 1/n
à l'ordinateur avec une précision donnée (par exemple de 12 digits),
cette série semble converger.
Exercice 3 (à rendre au début de la séance suivante)
Calculer avec un logiciel
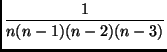
Exercice 4 (à rendre au début de la séance suivante)
Soit
0 ![]() q < 1 et un = qn. Déterminez un entier n0 tel que
q < 1 et un = qn. Déterminez un entier n0 tel que