suivant: Programme pour le polynôme
monter: Réduction exacte des endomorphismes
précédent: Réduction exacte des endomorphismes
Calcul du polynôme minimal
Soit 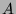 une matrice
une matrice 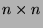 . Nous allons déterminer le polynôme
minimal de
. Nous allons déterminer le polynôme
minimal de 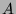 , c'est-à-dire un polynôme non nul de degré minimal
qui annule
, c'est-à-dire un polynôme non nul de degré minimal
qui annule 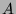 . On considère pour cela
. On considère pour cela 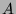 comme un vecteur
de l'espace des matrices ayant
comme un vecteur
de l'espace des matrices ayant 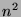 coordonnées (par exemple la matrice
identité en dimension 2 a pour coordonnées (1,0,0,1))
et on va chercher
par la méthode du pivot de Gauß une relation non triviale
entre les puissances successives de
coordonnées (par exemple la matrice
identité en dimension 2 a pour coordonnées (1,0,0,1))
et on va chercher
par la méthode du pivot de Gauß une relation non triviale
entre les puissances successives de 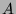 (on peut se limiter à
(on peut se limiter à 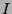 ,
,
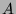 , ..,
, .., 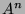 car le polynôme caractéristique de
car le polynôme caractéristique de 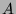 annule
annule 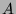 ).
).
Exercice 1 (à rendre à la fin de la 1ère séance de ce TP)
Soit la matrice :
Calculer à la calculatrice 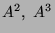 et appliquer le pivot de Gauß
sur les 4 lignes constituées par
et appliquer le pivot de Gauß
sur les 4 lignes constituées par
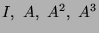 (si une colonne a des
zéros sur et sous la diagonale, on passe à la colonne suivante en
cherchant le pivot à partir de la même ligne).
(si une colonne a des
zéros sur et sous la diagonale, on passe à la colonne suivante en
cherchant le pivot à partir de la même ligne).
N'oubliez pas de garder une trace des opérations effectuées en notant
en bout de lignes l'expression des lignes (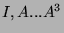 ).
).
Trouver le polynôme minimal de 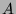 .
.
Trouver par la même méthode mais en faisant les calculs avec un logiciel
(HP49 instruction PMINI ou avec le programme MuPAD ci-dessous),
le polynôme minimal des matrices définies par :



suivant: Programme pour le polynôme
monter: Réduction exacte des endomorphismes
précédent: Réduction exacte des endomorphismes
2003-02-19