suivant: Cas où il y
monter: Méthode itératives
précédent: Méthode de la puissance.
La méthode des itérations inverses consiste lorsque l'endomorphisme 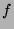 est inversible à appliquer l'algorithme de la puissance à
est inversible à appliquer l'algorithme de la puissance à 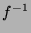 en effet:
en effet:
si 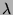 est une valeur propre de
est une valeur propre de 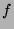 et si
et si  est un vecteur propre
associé à
est un vecteur propre
associé à 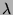 on a :
on a :
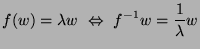
La méthode des itérations inverses permet donc de trouver la valeur
propre de plus petit module (à condition d'avoir inversé la matrice
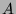 associée à
associée à 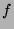 ).
).
La méthode des itérations inverses est utile
lorsqu'on connait une valeur approchée  d'une valeur propre
d'une valeur propre 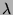 .
.
On
peut alors améliorer  en utilisant des itérations inverses,
puisqu'alors la matice
en utilisant des itérations inverses,
puisqu'alors la matice 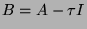 est inversible et possède
est inversible et possède 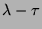 (qui est très petit) comme valeur propre.
(qui est très petit) comme valeur propre.
On cherche l'inverse de 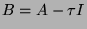 ,
puis on pose :
,
puis on pose :
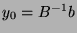 où
où 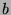 est un vecteur aléatoire (
est un vecteur aléatoire ( est alors
proche d'un vecteur propre correspondant à
est alors
proche d'un vecteur propre correspondant à
 .
.
On itère ensuite la procédure.
Exercice 4 (à rendre au plus tard le jour de l'examen)
Trouvez la plus petite valeur propre des matrices de l'exercice 3
(changez de matrice aléatoire si nécessaire).
Pour trouver les autres valeurs propres/vecteurs propres,
il faut pouvoir éliminer la valeur propre trouvée.
On sait en particulier le faire quand 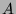 est symétrique,
car il suffit de remplacer
est symétrique,
car il suffit de remplacer 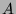 par
par
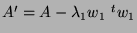 .
.
En effet, on prend une base orthonormale  de vecteurs
propres de
de vecteurs
propres de 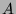 .
. 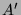 a les mêmes vecteurs propres que
a les mêmes vecteurs propres que 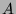 et pour
valeurs propres correspondantes
et pour
valeurs propres correspondantes  et les
et les 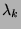 (
(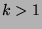 ) car pour
) car pour
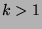 :
:
puisque 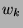 est orthogonal à
est orthogonal à 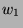
Exercice 5 (à rendre au plus tard le jour de l'examen)
Trouvez toutes les valeurs propres de la matrice :



suivant: Cas où il y
monter: Méthode itératives
précédent: Méthode de la puissance.
2003-02-19
![]() est symétrique,
car il suffit de remplacer
est symétrique,
car il suffit de remplacer ![]() par
par
![]() .
.
![]() de vecteurs
propres de
de vecteurs
propres de ![]() .
. ![]() a les mêmes vecteurs propres que
a les mêmes vecteurs propres que ![]() et pour
valeurs propres correspondantes
et pour
valeurs propres correspondantes ![]() et les
et les ![]() (
(![]() ) car pour
) car pour
![]() :
: