


suivant: Méthode itératives
monter: Réduction exacte des endomorphismes
précédent: Programme pour le polynôme
Recherche de vecteurs propres
On suppose que le polynôme minimal  est sans facteur carré
(square-free) ce qui se vérifie en cherchant le pgcd
de
est sans facteur carré
(square-free) ce qui se vérifie en cherchant le pgcd
de  avec sa dérivée.
À l'aide du polynôme minimal, il est facile de déterminer les
vecteurs propres de
avec sa dérivée.
À l'aide du polynôme minimal, il est facile de déterminer les
vecteurs propres de 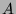 correspondant aux racines de
correspondant aux racines de  que l'on
sait déterminer car si
que l'on
sait déterminer car si
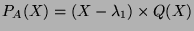 on a :
on a :
En effet puisque
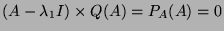 on a :
on a :
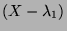 et
et 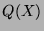 sont premiers entre eux car
sont premiers entre eux car  est sans facteur carré donc d'après Bézout,
il existe deux polynômes
est sans facteur carré donc d'après Bézout,
il existe deux polynômes 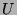 et
et  tels que :
tels que :
on a donc :
donc :
Lorsque le polynôme minimal n'est pas square-free, l'identité
de Bézout donne les projecteurs sur les espaces caractéristiques
(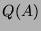 envoie
envoie 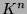 sur Ker
sur Ker
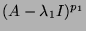 lorsque
lorsque 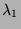 est
d'ordre
est
d'ordre 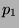 ).
).
Exercice 2 (ŕ rendre au plus tard le jour de l'examen)
Montrer que 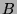 est diagonalisable et
trouver une base de vecteurs propres de la matrice
est diagonalisable et
trouver une base de vecteurs propres de la matrice 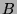 de l'exercice 1
en utilisant la méthode ci-dessus.
de l'exercice 1
en utilisant la méthode ci-dessus.



suivant: Méthode itératives
monter: Réduction exacte des endomorphismes
précédent: Programme pour le polynôme
2003-02-19
![]() est diagonalisable et
trouver une base de vecteurs propres de la matrice
est diagonalisable et
trouver une base de vecteurs propres de la matrice ![]() de l'exercice 1
en utilisant la méthode ci-dessus.
de l'exercice 1
en utilisant la méthode ci-dessus.