


suivant: Logiciels
monter: TP 3: Algèbre linéaire.
précédent: TP 3: Algèbre linéaire.
Rappels et définitions.
Pour diagonaliser un endomorphisme à la main,
on factorise le polynôme caractéristique det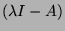 et on résoud
et on résoud
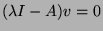 pour les racines
pour les racines 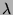 trouvées.
On va présenter d'autres méthodes plus efficaces à la machine ainsi
qu'une méthode numérique.
trouvées.
On va présenter d'autres méthodes plus efficaces à la machine ainsi
qu'une méthode numérique.
Définitions :
matrice caractéristique de 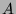 c'est
c'est 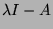
polynôme caractéristique de 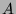 c'est det
c'est det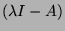 =
=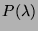
matrice adjointe de 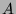 est la matrice des cofacteurs de la transposée
de
est la matrice des cofacteurs de la transposée
de 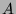 .
.
On a donc si 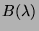 = matrice adjointe de
= matrice adjointe de 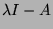 :
:
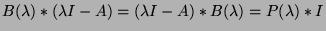
2003-02-19