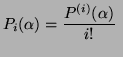On peut effectuer cette opération à nouveau sur ![]() , on obtient la
valeur de
, on obtient la
valeur de
![]() et un polynôme
et un polynôme ![]() , etc. jusqu'à obtenir
un polynôme de degré
, etc. jusqu'à obtenir
un polynôme de degré ![]() de degré 0.
de degré 0.
Exercice 4 (à rendre à la fin de la 2ème séance de TP) :
Pour quelle raison peut-on mettre en facteur ![]() dans
dans ![]() ?
?
Déterminer ![]() en fonction de
en fonction de ![]() puis pour
puis pour ![]() ,
, ![]() en fonction de
en fonction de ![]() et
et ![]() . Indiquez le détail des calculs
pour
. Indiquez le détail des calculs
pour
![]() et une valeur de
et une valeur de ![]() non nulle.
non nulle.
Calculer le nombre d'opérations effectuées avec cette méthode et
le nombre d'opérations que l'on effectuerait en évaluant le polynôme
sous forme développée, justifier l'intérêt de cette méthode.
Exercice 5 (à rendre à la fin de la 2ème séance de TP) :
Écrire un fonction effectuant ce calcul avec un logiciel de calcul formel :
on donnera en arguments le polynôme sous forme de la
liste de ces coefficients (dans l'exemple [1,2,0,-1,5]) et la
valeur de ![]() et le programme renverra
et le programme renverra
![]() et la liste des coefficients de
et la liste des coefficients de ![]() .
.
Exercice 6 (à rendre au début de la 3ème séance de TP) :
En utilisant la fonction de l'exercice précédent, écrire une fonction
qui prend en argument la liste des coefficients de ![]() et la valeur
de
et la valeur
de ![]() et renvoie la liste des valeurs
et renvoie la liste des valeurs
![]() , ...,
, ...,
![]() ,
, ![]() . Montrer que :
. Montrer que :